《2025年学霸提优大试卷七年级数学上册苏科版》

24. (9分)(1)观察思考:如图,线段 $ AB $ 上有两个点 $ C,D $,请分别写出以点 $ A,B,C,D $ 为左端点的线段,并计算图中共有多少条线段.
(2)模型构建:如果线段上有 $ m $ 个点(包括线段的两个端点),那么该线段上共有多少条线段?请说明你结论的正确性.
(3)拓展应用:某班45名同学在毕业后的一次聚会中,如果每两人握1次手问好,那么共握多少次手?请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.

答案：
(1)因为以点A为左端点的线段有线段AB,AC,AD,以点C为左端点的线段有线段CD,CB,以点D为左端点的线段有线段DB,所以共有3+2+1=6(条)线段　　
(2)共有$\frac{1}{2}$m(m−1)条线段.说明:设该线段上共有x条线段,则x=(m−1)+(m−2)+(m−3)+…+3+2+1，所以倒序排列有x=1+2+3+…+(m−3)+(m−2)+(m−1),所以x=$\frac{1}{2}$m(m−1).　　
(3)把45名同学看作直线上的45个点，每两名同学之间的一次握手看作一条线段，直线上45个点所构成的线段条数就等于握手的次数,因此一共要握手$\frac{1}{2}$×45×(45−1)=990(次).

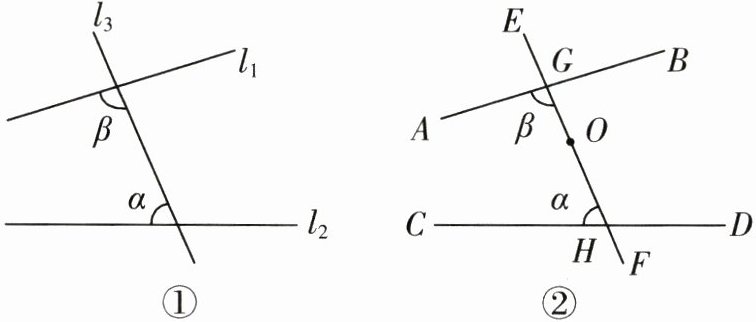
25. (10分)(2024·盐城盐都区期中)定义:若 $ \angle \alpha, \angle \beta $ 是同旁内角,并且 $ \angle \alpha, \angle \beta $ 满足 $ \angle \beta = \angle \alpha + 20^{\circ} $,则称 $ \angle \beta $ 是 $ \angle \alpha $ 的内联角.
(1)如图①,已知 $ \angle \beta $ 是 $ \angle \alpha $ 的内联角.
①当 $ \angle \alpha = 60^{\circ} $ 时,$ \angle \beta = $____$ ^{\circ} $;
②当直线 $ l_1 // l_2 $ 时,求 $ \angle \beta $ 的度数.
(2)如图②,已知 $ \angle \beta $ 是 $ \angle \alpha $ 的内联角,点 $ O $ 是线段 $ GH $ 上一定点.
①$ \angle DHG $ 是 $ \angle BGH $ 的内联角吗? 请说明理由.
②过点 $ O $ 的直线分别交直线 $ CD,AB $ 于点 $ P,Q $,若 $ \angle \alpha = 60^{\circ} $ 且 $ \angle EOP $ 是图中某个角的内联角,请直接写出 $ \angle EOP $ 是哪个角的内联角,以及此时 $ \angle EOP $ 的度数.

答案：

(1)①80　　[解析]∠β=∠α+20°=80°.　　②因为l₁//l₂,∠α,∠β是同旁内角,所以∠α+∠β=180°.因为∠β=∠α+20°,所以∠α+∠α+20°=180°,所以∠α=80°,所以∠β=∠α+20°=100°.　　
(2)①因为∠β=∠α+20°,∠DHG=180°−∠α,∠BGH=180°−∠β,所以∠DHG−∠BGH=∠β−∠α=20°,所以∠DHG=∠BGH+20°.又因为∠DHG与∠BGH是同旁内角,所以∠DHG是∠BGH的内联角.　　②∠EOP是∠CPO的内联角时,∠EOP=130°;∠EOP是∠DPO的内联角时,∠EOP=160°.　　[解析]点P在点H左侧如图①所示,此时有两种情况,当∠EOP是∠AGH的内联角时,∠EOP=∠β+20°=∠α+20°+20°=100°,此时PQ//AB,不符合题意;当∠EOP是∠CPO的内联角时,∠EOP=∠CPO+20°=60°+180°−∠EOP+20°=260°−∠EOP,解得∠EOP=130°;　　　　　　 　 　　点P在点H右侧如图②所示,因为∠AGH=∠α+20°=80°,∠CHG=60°,所以∠BGH=180°−∠AGH=100°,∠GHD=180°−∠CHG=120°,此时也有两种情况,当∠EOP是∠BGO的内联角时,∠EOP=∠BGO+20°=120°,所以∠EOP=∠GHD,所以PQ//CD,很显然不成立,故∠EOP=120°舍去;当∠EOP是∠DPO的内联角时,∠EOP=∠DPO+20°=120°+180°−∠EOP+20°=320°−∠EOP,解得∠EOP=160°.