《2025年学霸提优大试卷七年级数学上册苏科版》

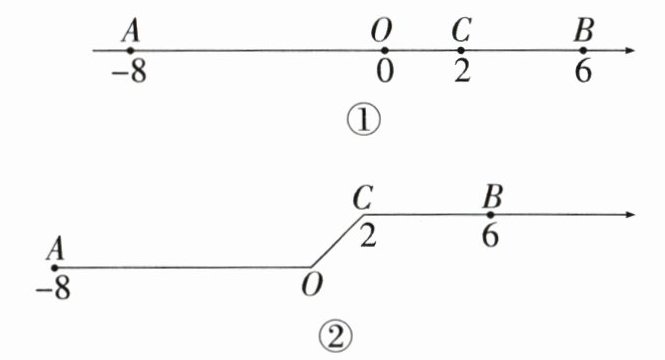
23. 数轴是一种特定的几何图形,利用数轴能形象地表示数,在关于数轴的问题中,我们常常用到数形结合的思想,并借助方程解决问题.如图①,在数轴上,点A表示的数为-8,点C表示的数为2,点B表示的数为6.
(1)点P从点A出发,以2个单位长度/秒的速度向右运动,同时,点Q从点B出发,以1个单位长度/秒的速度向左运动,经过多久两点相遇?
(2)如图②,我们将图①的数轴沿点O和点C各折一次后会得到一个新的图形,与原来相比,线段AO和CB仍然水平,线段OC处产生了一个坡度,我们称这样的数轴为“坡数轴”,其中O为“坡数轴”的原点,在“坡数轴”上,每个点对应的数就是把“坡数轴”拉直后对应的数.记“坡数轴”上点A到点B的距离$\overline {AB}$为A和B拉直后的距离,即$\overline {AB}= AO+OC+CB$,其中AO,OC,CB代表线段长度.在“坡数轴”上,上坡时点的移动速度变为水平路线上移动速度的一半,下坡时移动速度变为水平路线上移动速度的2倍.
①点P从点A出发,以2个单位长度/秒的速度沿着“坡数轴”向右运动,同时点Q从点B出发,以1个单位长度/秒的速度沿着“坡数轴”向左运动,经过多久,$\overline {PQ}= 3$?
②点P从A处沿“坡数轴”以每秒2个单位长度的速度向右移动,当移动到点C时,立即掉头返回(掉头时间不计),在点P出发的同时,点Q从点B处沿“坡数轴”以每秒1个单位长度的速度向左移动,当点P重新回到A点时,所有运动结束,设点P运动时间为t秒,在移动过程中,何时$\overline {PQ}= 3\overline {PO}$?

答案：
(1)设运动时间为$t$秒，点$P$与点$Q$相遇.因为点$P$从点$A$出发，以2个单位长度/秒的速度向右运动，点$Q$从点$B$出发，以1个单位长度/秒的速度向左运动，所以$2t + t=8 + 6$，解得$t=\frac{14}{3}$.所以点$P$与点$Q$经过$\frac{14}{3}$秒相遇.
(2)①当点$P$在$AO$上，点$Q$在$BC$上时，设点$P$与点$Q$运动的时间为$t$秒时，$PQ = 3$.因为$PQ=PO + OC + CQ=AO - AP + 2+BC - BQ$，得$8 - 2t+2 + 4 - t=3$，解得$t=\frac{11}{3}$.因为点$P$在$OC$上运动速度为1个单位长度/秒，点$Q$在$OC$上运动速度为2个单位长度/秒，由条件可知，当点$P$运动到$OC$中点时，点$Q$运动到点$O$，此时，$PQ = 1$.因为$AO = 8$，$OC = 2$，点$P$在$AO$上运动速度为2个单位长度/秒，在$OC$上运动速度为1个单位长度/秒，所以点$P$运动到$OC$中点所需时间为$\frac{8}{2}+1=5$（秒）.设点$P$运动到$OC$中点后，继续运动使得$PQ = 3$的时间为$t'$秒，因为点$Q$在$AO$上运动速度为1个单位长度/秒，此时$PQ=OQ + OP=t'+1 + t'=3$，所以$t' = 1$.所以经过$5 + 1=6$（秒），$PQ = 3$.综上，经过$\frac{11}{3}$秒或6秒，$PQ = 3$. ②(Ⅰ)当点$P$在$AO$上，点$Q$在$BC$上时，$PQ=PO + OC + CQ=(8 - 2t)+2+(4 - t)=14 - 3t$，$PO=8 - 2t$.因为$PQ = 3PO$，所以$14 - 3t=3(8 - 2t)$，所以$t=\frac{10}{3}$. (Ⅱ)当点$P$在$OC$上时，设从点$P$过$AO$，点$Q$过$BC$的4秒后的时间为$t'$秒. 1)当$OP + QC=OC$，即$t'+2t'=2$，即$t'=\frac{2}{3}$时，点$P,Q$相遇.$PQ=OC - OP - QC=2 - t'-2t'$，$PO=t'$.因为$PQ = 3PO$，所以$2 - t'-2t'=3t'$，解得$t'=\frac{1}{3}$.所以$t=4+\frac{1}{3}=\frac{13}{3}$. 2)当点$Q$到达点$O$时，点$P$恰好到达$OC$中点，并继续向上运动$2 - 1=1$（秒），$PQ=OP + OQ=t'+(t'-1)$，$PO=t'$.因为$PQ = 3PO$，所以$t'+(t'-1)=3t'$，解得$t'=-1$（舍去）. 3)当点$Q$在$OA$上，点$P$在$OC$上向下运动时，$PQ=OQ + OP=(t'-1)+[2 - 2×2(t'-2)]$，$PO=2 - 2×2(t'-2)$.因为$PQ = 3PO$，所以$(t'-1)+[2 - 2×2(t'-2)]=3×[2 - 2×2(t'-2)]$，解得$t'=\frac{7}{3}$.所以$t=4+\frac{7}{3}=\frac{19}{3}$. (Ⅲ)当点$P$重新运动至$OA$上时，设点$P$重新运动至点$O$后的运动时间为$t''$秒.在$t''$秒之前，点$P$、点$Q$已经运动了$4+2+\frac{1}{2}=\frac{13}{2}$（秒）.此时，点$Q$在$OA$上运动了$\frac{13}{2}-4 - 1=\frac{3}{2}$（秒），即$OQ=\frac{3}{2}×1=\frac{3}{2}$. a. 当点$P$在点$Q$右侧时，$PQ=OQ - OP=(\frac{3}{2}+t'')-2t''$，$PO=2t''$，因为$PQ = 3PO$，所以$(\frac{3}{2}+t'')-2t''=3×2t''$，解得$t''=\frac{3}{14}$.所以$t=\frac{13}{2}+\frac{3}{14}=\frac{47}{7}$. b. 当点$P$在点$Q$左侧，超过点$Q$后，$PQ=OP - OQ=2t''-(\frac{3}{2}+t'')$，$PO=2t''$，因为$PQ = 3PO$，所以$2t''-(\frac{3}{2}+t'')=3×2t''$，解得$t''=-\frac{3}{10}$（舍去）.综上，当$t=\frac{10}{3}$或$\frac{13}{3}$或$\frac{19}{3}$或$\frac{47}{7}$时，$PQ = 3PO$.