《2025年学霸提优大试卷七年级数学上册苏科版》

5. 算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹记数法中,以“纵式”和“横式”两种方式来表示数字,如图: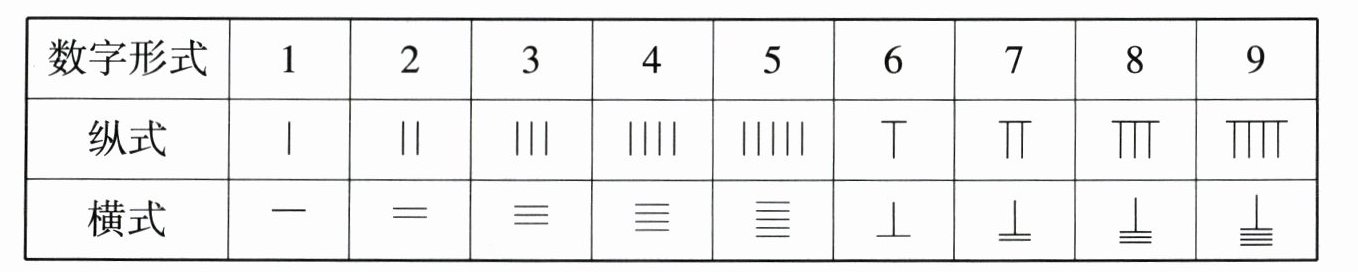
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例

则图中算筹所表示的数是9167.

答案： 9167 【解析】根据算筹记数法,表示的数是9167.

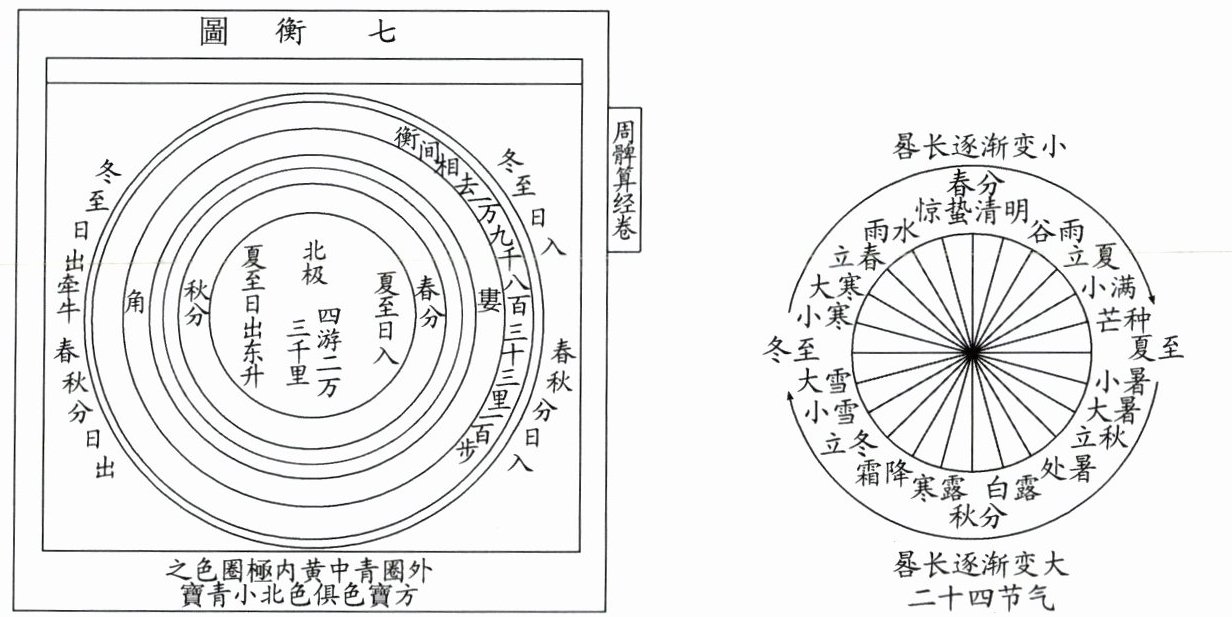
6. (2025·湖南模拟)《周髀算经》中的“七衡图”揭示了日晷(guǐ)的设计原理:一年有二十四个节气,二十四节气及晷长变化如图所示,上半年晷长逐渐变小,下半年晷长逐渐变大,周而复始.每个节气的晷长损益相同(晷长即为太阳光下晷针的影子长度,损益相同即为增加或减少的量相同).设每年冬至为第1个节气,晷长为一丈三尺五寸,夏至为第13个节气,晷长为一尺五寸,则第7个节气(春分)的晷长为7.5尺(一丈等于十尺,一尺等于十寸).

答案： 7.5 【解析】根据题意可知,从冬至到夏至晷长的变化次数为12次,而相邻两个节气晷长减少或增加的量均相同,所以每相邻两个节气晷长减少或增加的量为(13.5 - 1.5)÷12 = 1(尺),因此第7个节气(春分)的晷长为1.5+(13 - 7)×1 = 7.5(尺).

7. (2024·扬州江都区期末)中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人前三天走的路程为336里.

答案： 336 【解析】设第一天行走的路程为x里,由题意得,x + $\frac{1}{2}$x + $\frac{1}{4}$x + $\frac{1}{8}$x + $\frac{1}{16}$x + $\frac{1}{32}$x = 378,解得x = 192.则x + $\frac{1}{2}$x + $\frac{1}{4}$x = 192 + 96 + 48 = 336.即此人前三天走的路程为336里.

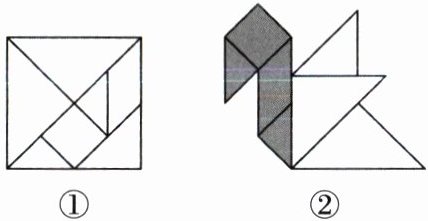
8. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板.用边长为8的正方形,做了如图①所示的七巧板.将这个七巧板拼成如图②所示的图形,则图②中阴影部分的面积为____.

答案：
24 【解析】如图,图②的阴影部分是由图①中1,2,3,4这四部分组成的,所以阴影部分的面积等于大正方形的面积减去两个大等腰直角三角形的面积,再减去中等的等腰直角三角形的面积,即阴影部分的面积 = 8×8 - $\frac{1}{2}$×8×8 - $\frac{1}{2}$×4×4 = 24.

9. 数列:$0,2,4,8,12,18,…$是我国的大衍数列,它也是世界数学史上第一道数列题.该数列中的奇数项和偶数项分别用代数式$\frac {n^{2}-1}{2},\frac {n^{2}}{2}$表示,如第1个数为$\frac {1^{2}-1}{2}= 0$,第2个数为$\frac {2^{2}}{2}= 2$,第3个数为$\frac {3^{2}-1}{2}= 4,…$,数轴上现有一点P从原点出发,依次以大衍数列中的数为距离向左右来回跳跃,第1秒时,点P在原点,记为$P_{1}$;第2秒点$P_{1}$向左跳2个单位长度,记为$P_{2}$,此时点$P_{2}$表示的数为-2;第3秒点$P_{2}$向右跳4个单位长度,记为$P_{3}$,点$P_{3}$表示的数为2……按此规律跳跃,点$P_{15}$表示的数为____.
56

答案： 56 【解析】这个大衍数列的前15个数分别是0,2,4,8,12,18,$\frac{7² - 1}{2}$ = 24,$\frac{8²}{2}$ = 32,$\frac{9² - 1}{2}$ = 40,$\frac{10²}{2}$ = 50,$\frac{11² - 1}{2}$ = 60,$\frac{12²}{2}$ = 72,$\frac{13² - 1}{2}$ = 84,$\frac{14²}{2}$ = 98,$\frac{15² - 1}{2}$ = 112,由题意得,点P₁₅表示的数为0 - 2 + 4 - 8 + 12 - 18 + 24 - 32 + 40 - 50 + 60 - 72 + 84 - 98 + 112 = (4 + 12 + 24 + 40 + 60 + 84 + 112) - (2 + 8 + 18 + 32 + 50 + 72 + 98) = 336 - 280 = 56.