《2025年学霸提优大试卷七年级数学上册苏科版》

10. (2024·北京平谷区模拟)我国古代数学著作《九章算术》里记载了这样一个有趣的问题:“今有善行者行100步,不善行者行60步.今不善行者先行100步,善行者追之,问几何步追之?”其意思是:走路快的人走100步时,走路慢的人只走了60步,现在走路慢的人先走100步,走路快的人去追他,问走路快的人走多少步能够追上他? 请你解决该问题.

答案： 设走路快的人要走x步才能追上对方,依题意,得$\frac{x}{100}$ = $\frac{x - 100}{60}$,解得x = 250.答:走路快的人要走250步才能追上走路慢的人.

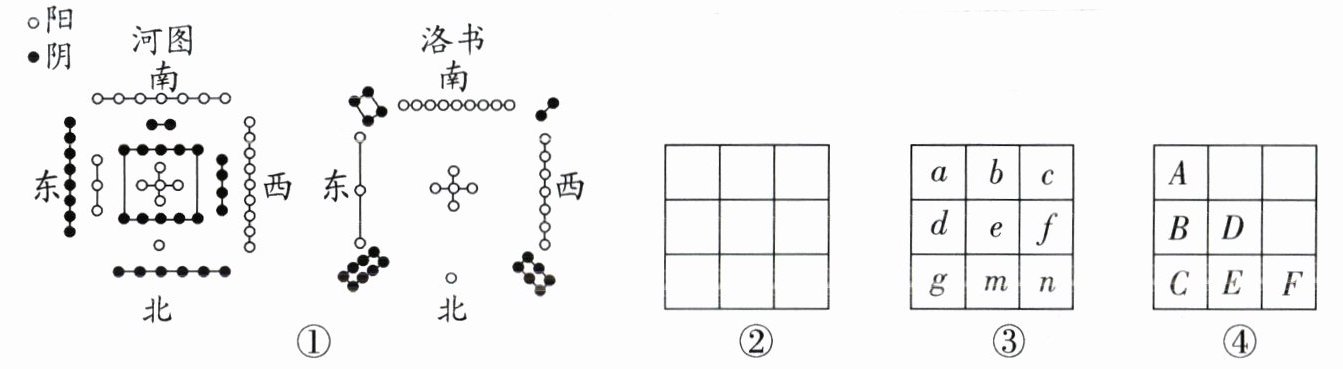
11. (2025·芜湖模拟)我国很多经典古籍中记载了“河图”和“洛书”,它是中国重要的文化遗产之一.“河图”和“洛书”中用实心点或空心点的个数表示数字.观察图①中的每一组点所对应的数字,回答下列问题:
(1)请按照图①“洛书”中的顺序把数字1~9填入图②对应的正方形空格中;
(2)我们把图②叫作一个“三阶”幻方.不难发现:“三阶”幻方的每行、每列、每条对角线上的数之和都相等.若将“三阶”幻方的每行、每列、每条对角线上三个数之和称为“幻方和”,中间的数称为“中心数”,则“幻方和”与“中心数”还存在着一定的倍数关系.
①如图③,已知$m = -2,c = -7$,幻方的“中心数”$e = -1$,则a的值为____;
②如图④,$A,B,C,D,E,F$是含有字母t的整式,$E = 4t,C = t + 3$,若幻方的“中心数”$D = m,B = -6t + m$,且m为常数,求m的值.

答案：

(1)如图①所示.

(2)①4 【解析】因为m + e + b = a + b + c,所以a = m + e - c = -2 + (-1) - (-7) = 4,所以a的值为4.②如图②.设“幻方和”为x,因为E = 4t,C = t + 3,D = m,B = -6t + m,所以A = x - B - C = x - (-6t + m) - (t + 3) = x + 5t - m - 3,M = x - D - E = x - 4t - m,G = x - B - D = x - (-6t + m) - m = x + 6t - 2m,H = x - C - D = x - (t + 3) - m = x - t - m - 3,F = x - C - E = x - (t + 3) - 4t = x - 5t - 3.因为A + D + F = x,所以x + 5t - m - 3 + m + x - 5t - 3 = x,所以x = 6.因为H + G + F = x,所以x - t - m - 3 + x + 6t - 2m + x - 5t - 3 = x,而x = 6,解得m = 2,所以m的值为2.