《2025年学霸提优大试卷七年级数学上册苏科版》

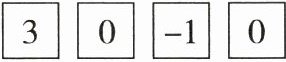
15. (8分)新情境(2025·张家口模拟)嘉嘉参加社会实践活动,按要求制作正方形木板,嘉嘉先制作了4块,木工师傅测量了边长,并记录了测量结果,如图所示(单位:mm),超过规定尺寸的记为正数,不足规定尺寸的记为负数,符合规定尺寸的记为“0”.
(1)通过列式,求这4块正方形木板中,最大块的边长比最小块多多少毫米.
(2)将符合规定尺寸的计为10分,不符合的不予计分,并依据测量结果执行扣分(每超过1mm扣1分,每不足1mm扣3分).
①嘉嘉制作的这4块正方形木板,可得多少分?
②后来嘉嘉又制作了2块正方形木板,这6块共得了22分,直接写出后来制作的2块的测量结果.

答案：
(1)由题意可得(+3)-(-1)=3+1=4(mm).故最大块边长比最小块多4 mm.
(2)①10×2-1×3-3×1=14(分).②原4块正方形木板得14分,现6块正方形木板得22分,故嘉嘉又制作了2块正方形木板,计8分,所以有1块合格的正方形木板和1块超过规定尺寸2 mm的正方形木板.

16. (12分)借助有理数的运算,对任意有理数a,b定义一种新运算“⊕”,规则如下:$a\oplus b= |a+b|$.例如,$2\oplus (-1)= |2+(-1)|= 1$.
(1)填空:①$5\oplus (-2)=$3;②若$3\oplus x= 4$,则$x=$1 或-7.
(2)我们知道有理数加法运算具有结合律,即$(a+b)+c= a+(b+c)$,请你探究这种新运算“⊕”是否也具有结合律.若具有,请说明理由;若不具有,请举一个例子说明.
新运算“⊕”不具有结合律,例子:因为[4⊕(-5)]⊕(-5)=|4+(-5)|⊕(-5)=1⊕(-5)=|1+(-5)|=4,4⊕[(-5)⊕(-5)]=4⊕|(-5)+(-5)|=4⊕10=|4+10|=14,所以[4⊕(-5)]⊕(-5)≠4⊕[(-5)⊕(-5)],所以新运算“⊕”不具有结合律.

答案：
(1)①3 【解析】因为a⊕b=|a+b|,所以5⊕(-2)=|5+(-2)|=3.②1 或-7 【解析】因为a⊕b=|a+b|,所以3⊕x=|3+x|=4,所以|3+x|=4,所以x₁=1,x₂=-7,所以x的值为1或-7.
(2)新运算“⊕”不具有结合律,例子:因为[4⊕(-5)]⊕(-5)=|4+(-5)|⊕(-5)=1⊕(-5)=|1+(-5)|=4,4⊕[(-5)⊕(-5)]=4⊕|(-5)+(-5)|=4⊕10=|4+10|=14,所以[4⊕(-5)]⊕(-5)≠4⊕[(-5)⊕(-5)],所以新运算“⊕”不具有结合律.

17. (12分)观察下列等式:
$\frac {1}{1×2}= 1-\frac {1}{2};\frac {1}{2×3}= \frac {1}{2}-\frac {1}{3};\frac {1}{3×4}= \frac {1}{3}-\frac {1}{4}$;可得$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}= 1-\frac {1}{2}+\frac {1}{2}-\frac {1}{3}+\frac {1}{3}-\frac {1}{4}= 1-\frac {1}{4}= \frac {3}{4}$.
(1)猜想并写出:$\frac {1}{99×100}=$$\frac{1}{99}-\frac{1}{100}$;
(2)利用上述猜想计算:$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+... +\frac {1}{99×100}$;
$\frac {1}{1×2}+\frac {1}{2×3}+\frac {1}{3×4}+…+\frac {1}{99×100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}$.
(3)探究并计算:$\frac {1}{2×4}+\frac {1}{4×6}+\frac {1}{6×8}+... +\frac {1}{2024×2026}$.
$\frac {1}{2×4}+\frac {1}{4×6}+\frac {1}{6×8}+…+\frac {1}{2024×2026}=\frac{1}{4}×(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{1012×1013})=\frac{1}{4}×(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{1012}-\frac{1}{1013})=\frac{1}{4}×(1-\frac{1}{1013})=\frac{1}{4}×\frac{1012}{1013}=\frac{253}{1013}$.

答案：
(1)$\frac{1}{99}-\frac{1}{100}$
(2)$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{99×100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}$.
(3)$\frac{1}{2×4}+\frac{1}{4×6}+\frac{1}{6×8}+…+\frac{1}{2024×2026}=\frac{1}{4}×(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{1012×1013})=\frac{1}{4}×(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{1012}-\frac{1}{1013})=\frac{1}{4}×(1-\frac{1}{1013})=\frac{1}{4}×\frac{1012}{1013}=\frac{253}{1013}$.