《2025年学霸提优大试卷七年级数学上册苏科版》

16. 如图是一个正方体积木,它的每个面上都有一个数字,其中1的对面是6,2的对面是5,3的对面是4.现将积木沿着地面标志翻转,最后朝上的面上的数字是____1.

答案： 1 【解析】根据题意可知,翻转第一次时3朝上;翻转第二次时5朝上;翻转第三次时4朝上;翻转第四次时6朝上;翻转第五次时3朝上;翻转第六次时1朝上.

17. 新趋势数学文化《冷庐杂识》有云:“近又有七巧图,其式五,其数七,其变化之式多至千余.”七巧板作为中国古老的益智玩具之一,已有千年的历史,素有“来自中国的拼图”“东方魔板”之称,是世界公认的中国优秀智力玩具代表作.如图,小明拼凑出爱心形状,若爱心的面积为48,那么七巧板中正方形GKHC的面积为____.

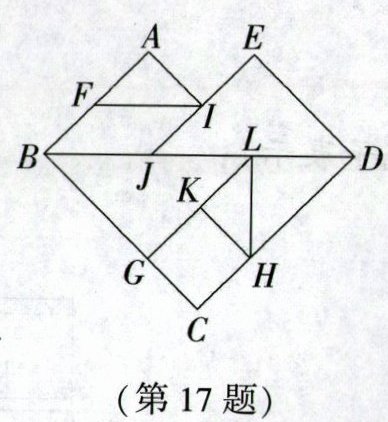
答案：
6 【解析】设$\triangle KLH$的面积为x,结合七巧板的性质得各个面积的情况如图所示,依题意,$4x+4x+2x+2x+2x+x+x=16x=48$,解得$x=3$,所以正方形GKHC的面积为$3×2=6$.

18. 点动成线,线动成面,面动成体,立体之美,无处不在,需要我们会用数学的眼光观察现实世界.如图,直角三角形ABC绕AB边所在直线旋转一周所得的圆锥放到一个盛有水的圆柱形容器中,完全浸没,水面上升至8cm,则未放入圆锥前圆柱形容器内的水面高度为____6.72cm.$(V_{圆柱}= πr^{2}h,V_{圆锥}= \frac{1}{3}πr^{2}h,r$为圆柱和圆锥底面半径,h为圆柱和圆锥的高$)$

答案： 6.72 【解析】设未放入圆锥前圆柱形容器内的水高度为h cm,圆锥的体积为$\frac{1}{3}\pi×4^{2}×6=32\pi(\text{cm}^3)$.由题意可得$\pi×\left(\frac{10}{2}\right)^{2}×8=32\pi+\pi×\left(\frac{10}{2}\right)^{2}× h$,解得$h=6.72$.故未放入圆锥前圆柱形容器内的水面高度为6.72 cm.

19. (4分)如图,方格纸上画出了一棵树的一半,将其沿树干翻折,画出翻折后的图形.

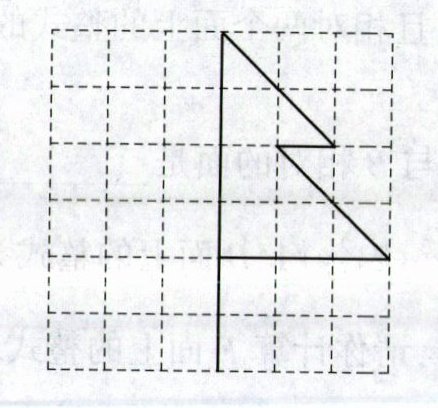
答案：
如图所示:

20. (6分)(2024·西安校级模拟)如图,某酒店大堂的旋转门内部由三块宽为1.8m、高为3m的玻璃隔板组成.
(1)将此旋转门旋转一周,能形成的几何体是____圆柱,这能说明的事实是____C(填字母);
A. 点动成线 B. 线动成面 C. 面动成体
(2)求该旋转门旋转一周形成的几何体的体积.(边框及衔接处忽略不计,结果保留π)

该旋转门旋转一周形成的几何体是圆柱，体积为$\pi×1.8^{2}×3 = 9.72\pi(\text{m}^3)$。故形成的几何体的体积是$9.72\pi \,\text{m}^3$。

答案：
(1)圆柱 C 【解析】因为旋转门的形状是长方形,所以旋转门旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体.
(2)该旋转门旋转一周形成的几何体是圆柱,体积为$\pi×1.8^{2}×3=9.72\pi(\text{m}^3)$.故形成的几何体的体积是$9.72\pi \,\text{m}^3$.