《2025年自主学习指导课程与测试八年级数学上册人教版》

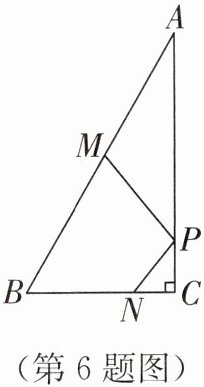
6. 如图，在 $ Rt \triangle ABC $ 中，$ \angle C = 90^{\circ} $，$ \angle A = 30^{\circ} $，点 $ N $ 在边 $ BC $ 上，且 $ BN = 6 $，点 $ M $，$ P $ 分别是边 $ AB $，$ AC $ 上的动点，当 $ PM + PN $ 最小时，$ BM = 5 $，则 $ AB $ 长为(D)

A.10
B.12
C.14
D.16

答案： 6.D

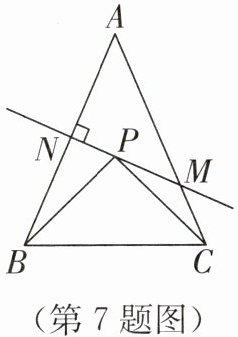
7. 如图，在 $ \triangle ABC $ 中，已知 $ AB = AC = 8 $，$ BC = 5 $，$ AB $ 的垂直平分线交 $ AB $ 于点 $ N $，交 $ AC $ 于点 $ M $，$ P $ 为直线 $ MN $ 上一点，连接 $ PB $，$ PC $，则 $ \triangle PBC $ 的周长最小值是13.

答案： 7.13

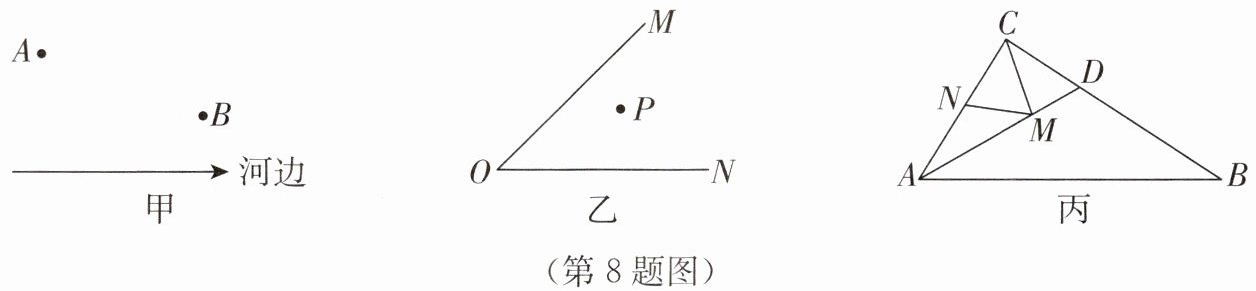
8. (1) 唐朝诗人李颀的诗《古从军行》开头两句：“白日登山望烽火，黄昏饮马傍交河”，诗中隐含着一个有趣的数学问题：如图甲所示，诗中大意是将军从山脚下的 $ A $ 点出发，带着马走到河边 $ P $ 点饮水后，再回到 $ B $ 点宿营，请问将军怎样走才能使总路程最短？请你通过画图，在图中找出 $ P $ 点，使 $ PA + PB $ 的值最小，不说明理由.
(2) 实践应用 1：如图乙，点 $ P $ 为 $ \angle MON $ 内一点，请在射线 $ OM $，$ ON $ 上分别找到两点 $ A $，$ B $，使 $ \triangle PAB $ 的周长最小，不说明理由.
(3) 实践应用 2：如图丙，在 $ \triangle ABC $ 中，$ AC = 6 $，$ BC = 8 $，$ AB = 10 $，$ \angle ACB = 90^{\circ} $，$ AD $ 平分 $ \angle BAC $，$ M $，$ N $ 分别是 $ AD $，$ AC $ 边上的动点，求 $ CM + MN $ 的最小值.

答案：
8.解:
(1)如图1:
　　　　　　　　　　　　　　
(2)如图2:
　　　　　　　　　　　　　　
(3)如图3,过点C作$CE\perp AD$,交AB于E,AD于O,连接ME,则$CM+MN$最小.
　　$\therefore \angle AOC=\angle AOE=90^{\circ}$.
　　$\because$AD平分$\angle BAC$,
　　$\therefore \angle CAD=\angle BAD$.
　　在$\triangle AOC$和$\triangle AOE$中,$\begin{cases} \angle CAD=\angle BAD, \\ AO=AO, \\ \angle AOC=\angle AOE, \end{cases}$
　　$\therefore \triangle AOC\cong \triangle AOE(ASA)$.
　　$\therefore OC=OE$,$AE=AC=6$.
　　$\because \angle AOC=\angle AOE=90^{\circ}$,$OM=OM$,
　　$\therefore \triangle COM\cong \triangle EOM$.
　　$\therefore CM=EM$.
　　$\therefore CM+MN=EM+MN\geqslant EN$.
　　$\therefore$当点N,M,E共线时,$CM+MN$最小,最小值为EN,且当$EN\perp AC$时,NE最小.
　　过点C作$CF\perp AB$于点F,
　　$\because AC=6$,$BC=8$,$AB=10$,$\angle ACB=90^{\circ}$,
　　$\therefore S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CF$.
　　即$\frac{1}{2}×6×8=\frac{1}{2}×10× CF$,
　　解得$CF=\frac{24}{5}$,
　　$\because S_{\triangle AEC}=\frac{1}{2}AC\cdot NE=\frac{1}{2}AE\cdot CF$,
　　$\therefore EN=\frac{24}{5}$.