第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
7. 任意两个奇数的平方差总能(
A.被 3 整除
B.被 5 整除
C.被 6 整除
D.被 8 整除
D
)A.被 3 整除
B.被 5 整除
C.被 6 整除
D.被 8 整除
答案:
7.D
8. 如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如$4 = 2^{2}-0^{2}$,$12 = 4^{2}-2^{2}$,$20 = 6^{2}-4^{2}$,因此 4,12,20 都是“神秘数”,则下面数是“神秘数”的是(
A.56
B.66
C.76
D.86
C
)A.56
B.66
C.76
D.86
答案:
8.C
9. 从前,古希腊的一位庄园主人把一块边长为$a$m($a>8$)的正方形土地租给租户约翰,第二年,他对约翰说:“我把这块地一边增加 8 m,另外一边减少 8 m,变成长方形土地,继续原价租给你,你看如何?”若是这样,你认为约翰吃亏了吗?通过计算说明你的结论.
答案:
9.解:约翰吃亏了.理由如下:
原正方形的面积(单位:m²)为a²,
改变边长后面积(单位:m²)为(a + 8)(a - 8)=a² - 64.
∵$a² - 64\lt a²,$
∴约翰吃亏了.
原正方形的面积(单位:m²)为a²,
改变边长后面积(单位:m²)为(a + 8)(a - 8)=a² - 64.
∵$a² - 64\lt a²,$
∴约翰吃亏了.
10. 计算:
(1)$(a - 2b)(-2b - a)-(3a + 4b)(-3a + 4b)$;
(2)$(x - \frac{1}{2})(x^{2}+\frac{1}{4})(x + \frac{1}{2})$.
(1)$(a - 2b)(-2b - a)-(3a + 4b)(-3a + 4b)$;
(2)$(x - \frac{1}{2})(x^{2}+\frac{1}{4})(x + \frac{1}{2})$.
答案:
$(1)$ 计算$(a - 2b)(-2b - a)-(3a + 4b)(-3a + 4b)$
解:
根据平方差公式$(m+n)(m - n)=m^{2}-n^{2}$。
对于$(a - 2b)(-2b - a)$,可变形为$(-2b + a)(-2b - a)$,这里$m=-2b$,$n = a$,则$(-2b + a)(-2b - a)=(-2b)^{2}-a^{2}=4b^{2}-a^{2}$。
对于$(3a + 4b)(-3a + 4b)$,可变形为$(4b + 3a)(4b - 3a)$,这里$m = 4b$,$n = 3a$,则$(4b + 3a)(4b - 3a)=(4b)^{2}-(3a)^{2}=16b^{2}-9a^{2}$。
将上述结果代入原式可得:
$\begin{aligned}&(a - 2b)(-2b - a)-(3a + 4b)(-3a + 4b)\\=&4b^{2}-a^{2}-(16b^{2}-9a^{2})\\=&4b^{2}-a^{2}-16b^{2}+9a^{2}\\=&(9a^{2}-a^{2})+(4b^{2}-16b^{2})\\=&8a^{2}-12b^{2}\end{aligned}$
$(2)$ 计算$(x - \frac{1}{2})(x^{2}+\frac{1}{4})(x + \frac{1}{2})$
解:
根据乘法交换律,先计算$(x - \frac{1}{2})(x + \frac{1}{2})$,这里$m=x$,$n=\frac{1}{2}$,由平方差公式$(m+n)(m - n)=m^{2}-n^{2}$可得:
$(x - \frac{1}{2})(x + \frac{1}{2})=x^{2}-(\frac{1}{2})^{2}=x^{2}-\frac{1}{4}$
再计算$(x^{2}-\frac{1}{4})(x^{2}+\frac{1}{4})$,这里$m = x^{2}$,$n=\frac{1}{4}$,由平方差公式可得:
$(x^{2}-\frac{1}{4})(x^{2}+\frac{1}{4})=(x^{2})^{2}-(\frac{1}{4})^{2}=x^{4}-\frac{1}{16}$
综上,$(1)$的结果为$\boldsymbol{8a^{2}-12b^{2}}$;$(2)$的结果为$\boldsymbol{x^{4}-\frac{1}{16}}$。
解:
根据平方差公式$(m+n)(m - n)=m^{2}-n^{2}$。
对于$(a - 2b)(-2b - a)$,可变形为$(-2b + a)(-2b - a)$,这里$m=-2b$,$n = a$,则$(-2b + a)(-2b - a)=(-2b)^{2}-a^{2}=4b^{2}-a^{2}$。
对于$(3a + 4b)(-3a + 4b)$,可变形为$(4b + 3a)(4b - 3a)$,这里$m = 4b$,$n = 3a$,则$(4b + 3a)(4b - 3a)=(4b)^{2}-(3a)^{2}=16b^{2}-9a^{2}$。
将上述结果代入原式可得:
$\begin{aligned}&(a - 2b)(-2b - a)-(3a + 4b)(-3a + 4b)\\=&4b^{2}-a^{2}-(16b^{2}-9a^{2})\\=&4b^{2}-a^{2}-16b^{2}+9a^{2}\\=&(9a^{2}-a^{2})+(4b^{2}-16b^{2})\\=&8a^{2}-12b^{2}\end{aligned}$
$(2)$ 计算$(x - \frac{1}{2})(x^{2}+\frac{1}{4})(x + \frac{1}{2})$
解:
根据乘法交换律,先计算$(x - \frac{1}{2})(x + \frac{1}{2})$,这里$m=x$,$n=\frac{1}{2}$,由平方差公式$(m+n)(m - n)=m^{2}-n^{2}$可得:
$(x - \frac{1}{2})(x + \frac{1}{2})=x^{2}-(\frac{1}{2})^{2}=x^{2}-\frac{1}{4}$
再计算$(x^{2}-\frac{1}{4})(x^{2}+\frac{1}{4})$,这里$m = x^{2}$,$n=\frac{1}{4}$,由平方差公式可得:
$(x^{2}-\frac{1}{4})(x^{2}+\frac{1}{4})=(x^{2})^{2}-(\frac{1}{4})^{2}=x^{4}-\frac{1}{16}$
综上,$(1)$的结果为$\boldsymbol{8a^{2}-12b^{2}}$;$(2)$的结果为$\boldsymbol{x^{4}-\frac{1}{16}}$。
11. 从边长为$a$的正方形中剪掉一个边长为$b$的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
(1)上述操作能验证的等式是
(2)已知$4a^{2}-24 = b^{2}$,$2a + b = 6$,则$2a - b=$
(3)应用所得的公式计算:$2025^{2}-2024×2026$.
(4)应用所得的公式计算:$9×(10 + 1)×(10^{2}+1)×(10^{4}+1)×(10^{8}+1)×(10^{16}+1)+1$.
]
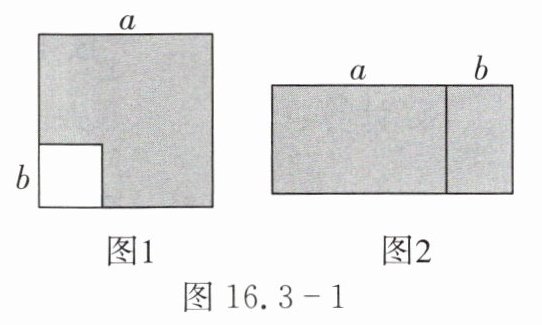
(1)上述操作能验证的等式是
a² - b²=(a + b)(a - b)
;(用含$a$,$b$的等式表示)(2)已知$4a^{2}-24 = b^{2}$,$2a + b = 6$,则$2a - b=$
4
;(3)应用所得的公式计算:$2025^{2}-2024×2026$.
(4)应用所得的公式计算:$9×(10 + 1)×(10^{2}+1)×(10^{4}+1)×(10^{8}+1)×(10^{16}+1)+1$.
]

答案:
11.解:
(1)a² - b²=(a + b)(a - b);
(2)4;
(3)2025² - 2024×2026=2025² - (2025 - 1)×(2025 + 1)=2025² - (2025² - 1²)=2025² - 2025² + 1=1;
(4)9×(10 + 1)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10 - 1)×(10 + 1)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10² - 1²)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10⁴ - 1⁴)×(10⁴ + 1⁴)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10⁸ - 1⁸)×(10⁸ + 1⁸)×(10¹⁶ + 1)+1
=(10¹⁶ - 1¹⁶)×(10¹⁶ + 1¹⁶)+1
=10³² - 1³² + 1
=10³².
(1)a² - b²=(a + b)(a - b);
(2)4;
(3)2025² - 2024×2026=2025² - (2025 - 1)×(2025 + 1)=2025² - (2025² - 1²)=2025² - 2025² + 1=1;
(4)9×(10 + 1)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10 - 1)×(10 + 1)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10² - 1²)×(10² + 1)×(10⁴ + 1)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10⁴ - 1⁴)×(10⁴ + 1⁴)×(10⁸ + 1)×(10¹⁶ + 1)+1
=(10⁸ - 1⁸)×(10⁸ + 1⁸)×(10¹⁶ + 1)+1
=(10¹⁶ - 1¹⁶)×(10¹⁶ + 1¹⁶)+1
=10³² - 1³² + 1
=10³².
查看更多完整答案,请扫码查看


