第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
$8. i ^ { 2 } = - 1 ,$并且$ i $满足学过的运算律,则$ ( 1 + i ) \cdot ( 2 - i ) $运算结果是$($
A. 3 - i
B. 2 + i
C. 1 - i
D. 3 + i
$D$
$)$ A. 3 - i
B. 2 + i
C. 1 - i
D. 3 + i
答案:
8.D
$9. $已知$ a b = a + b + 1 ,$则$ ( a - 1 ) ( b - 1 ) = $
$2$
$.$
答案:
9.2
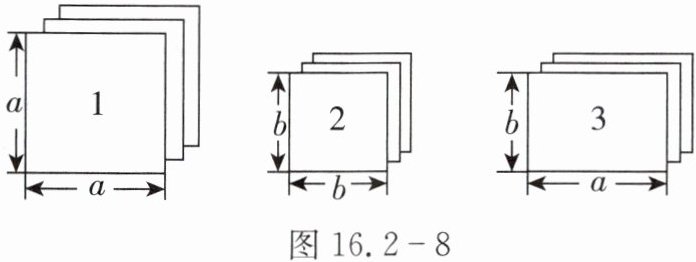
$10. $如图$16.2-8,$有足够多的长方形和正方形卡片,
$(1) $如果选取$1$号,$2$号,$3$号卡片分别为$1$张,$3$张,$4$张,可拼成一个长方形$($不重叠无缝隙$),$请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形所表示的一个等式;
$(2) $小明想用类似方法解释多项式乘法$ ( a + 3 b ) ( 2 a + b ) = 2 a ^ { 2 } + 7 a b + 3 b ^ { 2 } ,$那么需用$1$号卡片
$(1) $如果选取$1$号,$2$号,$3$号卡片分别为$1$张,$3$张,$4$张,可拼成一个长方形$($不重叠无缝隙$),$请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形所表示的一个等式;
$(2) $小明想用类似方法解释多项式乘法$ ( a + 3 b ) ( 2 a + b ) = 2 a ^ { 2 } + 7 a b + 3 b ^ { 2 } ,$那么需用$1$号卡片
$2$
张,$2$号卡片 $3$
张,$3$号卡片 $7$
张$.$ 
答案:
$10.(1)(a + b)(a + 3b)=a^{2}+4ab + 3b^{2} $画图如右图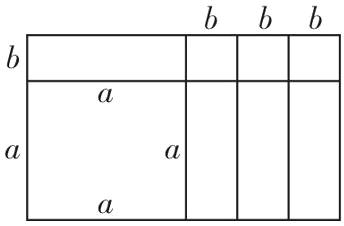
(2)2 3 7
$10.(1)(a + b)(a + 3b)=a^{2}+4ab + 3b^{2} $画图如右图

(2)2 3 7
$11. $我国南宋时期杰出的数学家杨辉$($钱塘$($今杭州$)$人$),$下面的图表是他在$《$详解九章算术$》$中记载的$“$杨辉三角$”.$

此图揭示了$ ( a + b ) ^ { n } ( n $为非负整数$)$的展开式的项数及各项系数的有关规律,由此规律可解决如下问题:假如今天是星期三,再过$7$天还是星期三,那么再过$ 8 ^ { 2025 } $天是星期几$?$

此图揭示了$ ( a + b ) ^ { n } ( n $为非负整数$)$的展开式的项数及各项系数的有关规律,由此规律可解决如下问题:假如今天是星期三,再过$7$天还是星期三,那么再过$ 8 ^ { 2025 } $天是星期几$?$
答案:
11.解:
∵$8^{2025}=(7 + 1)^{2025}=7^{2025}+m×7^{2024}×1^{1}+n×7^{2023}×1^{2}+p×7^{2022}×1^{3}+⋯+q×7×1^{2024}+1^{2025},$其中m,n,p,q为常数,
∴$8^{2025}$除以7的余数为1.
∵今天是星期三,再过7天还是星期三,
∴再过$8^{2025}$天是星期四.
∵$8^{2025}=(7 + 1)^{2025}=7^{2025}+m×7^{2024}×1^{1}+n×7^{2023}×1^{2}+p×7^{2022}×1^{3}+⋯+q×7×1^{2024}+1^{2025},$其中m,n,p,q为常数,
∴$8^{2025}$除以7的余数为1.
∵今天是星期三,再过7天还是星期三,
∴再过$8^{2025}$天是星期四.
$12. $观察:
$ ( x - 1 ) ( x + 1 ) = x ^ { 2 } - 1 ,$$ ( x - 1 ) ( x ^ { 2 } + x + 1 ) = x ^ { 2 } - 1 ,$
$ ( x - 1 ) ( x ^ { 3 } + x ^ { 2 } + x + 1 ) = x ^ { 4 } - 1 ,$$ ( x - 1 ) ( x ^ { 3 } + x ^ { 3 } + x ^ { 2 } + x + 1 ) = x ^ { 5 } - 1 ,$
$…$
利用以上规律确定$ 2 ^ { 2025 } + 2 ^ { 2024 } + 2 ^ { 2023 } + \cdots + 2 ^ { 2 } + 2 + 1 $的个位数字是
$ ( x - 1 ) ( x + 1 ) = x ^ { 2 } - 1 ,$$ ( x - 1 ) ( x ^ { 2 } + x + 1 ) = x ^ { 2 } - 1 ,$
$ ( x - 1 ) ( x ^ { 3 } + x ^ { 2 } + x + 1 ) = x ^ { 4 } - 1 ,$$ ( x - 1 ) ( x ^ { 3 } + x ^ { 3 } + x ^ { 2 } + x + 1 ) = x ^ { 5 } - 1 ,$
$…$
利用以上规律确定$ 2 ^ { 2025 } + 2 ^ { 2024 } + 2 ^ { 2023 } + \cdots + 2 ^ { 2 } + 2 + 1 $的个位数字是
$3$
$.$
答案:
12.3
查看更多完整答案,请扫码查看


