《2025年新课程学习指导高中数学必修第二册北师大版》

1. 如图为一个缆车示意图，该缆车半径为4.8m，圆上最低点与地面的距离为0.8m，60s转动一圈，图中OA与地面垂直，以OA为始边，逆时针转动θ角到OB，设点B与地面距离是h。

(1)求h与θ之间的函数解析式；
(2)设从OA开始转动，经过ts后到达OB，求h与t之间的函数解析式，并求缆车到达最高点时用的最少时间。

答案：
解:
(1) 以圆心 $O$ 为原点，建立如图所示的坐标系，则以 $Ox$ 为始边，$OB$ 为终边的角为 $\theta - \frac{\pi}{2}$。

故点 $B$ 的坐标为 $(4.8\cos(\theta - \frac{\pi}{2}), 4.8\sin(\theta - \frac{\pi}{2}))$。
$\therefore h = 5.6 + 4.8\sin(\theta - \frac{\pi}{2})$。
(2) 点 $A$ 在圆上转动的角速度是 $\frac{\pi}{30}$，故 $t\ s$ 转过的弧度数为 $\frac{\pi t}{30}$。
$\therefore h = 5.6 + 4.8\sin(\frac{\pi}{30}t - \frac{\pi}{2})$，$t \in [0, +\infty)$。
到达最高点时，$h = 10.4\ m$。
由 $\sin(\frac{\pi}{30}t - \frac{\pi}{2}) = 1$，得 $\frac{\pi}{30}t - \frac{\pi}{2} = 2k\pi + \frac{\pi}{2}(k \in Z)$。
当 $k = 0$ 时，缆车到达最高点时用的时间最少，此时 $t = 30\ s$。
$\therefore$ 缆车到达最高点时，用的最少时间是 $30\ s$。

2. 如图，在矩形ABCD中，AB = 1，BC = $\sqrt{3}$，此矩形沿地面上一直线滚动，在滚动过程中，矩形ABCD所在的平面始终与地面垂直，设直线BC与地面所成的角为θ，矩形周边上最高点离地面的距离为f(θ)。

求：(1)θ的取值范围；
(2)f(θ)的解析式；
(3)f(θ)的值域。

答案：
解:
(1) 观察可知 $BC$ 与地面所成的角 $\theta$ 的取值范围为 $[0, \frac{\pi}{2}]$。

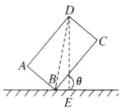
(2) 如图，连接 $BD$，在 $Rt\triangle BCD$ 中，$CD = 1$，$BC = \sqrt{3}$，则 $\angle DBC = \frac{\pi}{6}$。
过点 $D$ 作地面的垂线，垂足为 $E$，在 $Rt\triangle BED$ 中，$\angle DBE = \theta + \frac{\pi}{6}$，$DB = 2$。
$\therefore f(\theta) = 2\sin(\theta + \frac{\pi}{6})(0 \leq \theta \leq \frac{\pi}{2})$。
(3) 由
(2) 知，当 $0 \leq \theta \leq \frac{\pi}{2}$ 时，$\frac{\pi}{6} \leq \theta + \frac{\pi}{6} \leq \frac{2\pi}{3}$。
$\therefore \frac{1}{2} \leq \sin(\theta + \frac{\pi}{6}) \leq 1$，即 $f(\theta)$ 的值域为 $[1, 2]$。