《2025年新课程学习指导高中数学必修第二册北师大版》

2.圆柱、圆锥、圆台的性质:
(1)平行于圆柱、圆锥、圆台的底面的截面都是圆面;
(2)过圆柱、圆锥、圆台旋转轴的截面分别是____________ __________________、______________.
[微思考]　　连接圆柱(或圆台)上、下底面圆周上各一点构成的线段，是否一定为母线？
　　______________________________

答案：
(2)全等的矩形、等腰三角形、等腰梯形
[微思考]
提示:不一定。连接圆柱(圆台)上、下底面圆周上两点的线段不一定在侧面上，因此不一定是母线。

1.下列图形中是圆柱的是　　　　　　　　　(　　　)

答案： B

2.过圆锥的轴作截面，则截面形状一定是(　　　)
A.直角三角形　　　　　　B.等腰三角形
C.等边三角形　　　　　　　D.等腰直角三角形

答案： B

[典例1]　下列说法正确的是　　　(　　　)
A.圆锥的底面是圆面，侧面是曲面
B.用一张扇形的纸片可以卷成一个圆锥
C.一个物体上、下两个面是相等的圆面,那么它一定是一个圆柱
D.球面上四个不同的点一定不在同一平面内

答案： A

1. 下列命题正确的是　　　　　　　　　　(　　　)
①过球面上任意两点只能作一个经过球心的圆；②以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的旋转体叫作球体，半圆的直径叫作球的直径；③用不过球心的截面截球，球心和截面圆心的连线垂直于截面；④球面上任意三点可能在一条直线上；⑤球的半径是连接球面上任意一点和球心的线段。
A. ①②③　B. ②③④　C. ②③⑤　D. ①④⑤

答案： C

2. 下列命题正确的是　　　　　　　　　　(　　　)
A. 圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线
B. 一直角梯形绕下底所在直线旋转一周，所形成的曲面围成的几何体是圆台
C. 圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都可以构成直角三角形
D. 用平面去截圆锥一定会得到一个圆锥和一个圆台

答案： C

[典例2]　用一个平面截半径为25cm的球，截面面积是49πcm²，求球心到截面的距离。

答案：
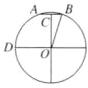
解:如图，作出球的轴截面，由题意知OB = r = 25，π·BC² = 49π，
∴BC = 7，　　　　
∴OC = $\sqrt{OB^{2}-BC^{2}}$ = $\sqrt{25^{2}-7^{2}}$ = 24
因此，球心到截面的距离为24cm。