《2025年名校课堂九年级数学全一册湘教版广西专版》

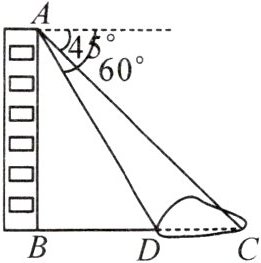
6. (2024·贵港桂平市期末)如图，从楼顶A处看楼下荷塘C处的俯角为45°，看楼下荷塘D处的俯角为60°，已知楼高AB为30米，则荷塘的宽CD为(30-10√3)米(结果保留根号).

答案： (30-10√3)

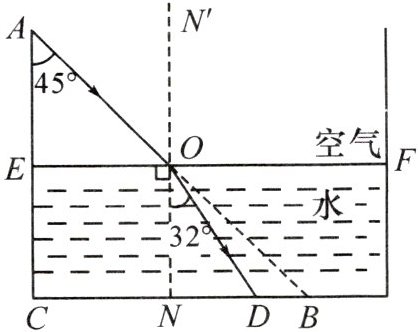
7. 新考向 跨学科(2024·贵州)综合与实践：小星学习解直角三角形的知识后，结合光的折射规律进行了如下综合性学习.
【实验操作】
第一步：将长方体空水槽放置在水平桌面上，一束光线从水槽边沿A处投射到底部B处，入射光线与水槽内壁AC的夹角为$\angle A$；
第二步：向水槽注水，当水面上升到AC的中点E处时，停止注水.(直线NN'为法线，AO为入射光线，OD为折射光线)
【测量数据】
如图，点A，B，C，D，E，F，O，N，N'在同一平面内，测得AC=20cm，$\angle A=45^{\circ}$，折射角$\angle DON=32^{\circ}$.
【问题解决】
根据以上实验操作和测量的数据，解答下列问题：
(1)求BC的长；
(2)求B，D之间的距离.(结果精确到0.1cm.参考数据：$\sin32^{\circ}\approx0.53$，$\cos32^{\circ}\approx0.85$，$\tan32^{\circ}\approx0.62$)

答案：
(1)在$Rt\triangle ABC$中,$\angle A=45°$,$\therefore\angle B=45°$.$\therefore BC=AC=20\ cm$.
(2)由题意可知,$ON=EC=\frac{1}{2}AC=10\ cm$,$\therefore BN=ON=10\ cm$.在$Rt\triangle OND$中,$\because\angle DON=32°$,$\therefore DN=ON\cdot\tan\angle DON=10\cdot\tan32°\approx10×0.62=6.2(cm)$.$\therefore BD=BN-DN\approx10-6.2=3.8(cm)$.$\therefore B,D$之间的距离约为3.8 cm.

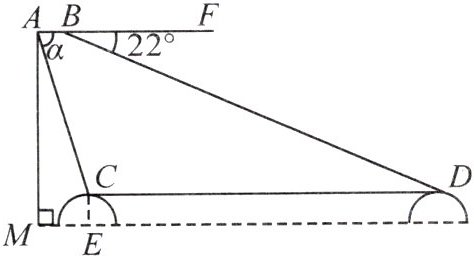
8. (2024·贵港桂平市期末)如图，某校数学兴趣小组借助无人机测量某隧道的长度CD，一架水平飞行的无人机在A处测得正前方隧道的入口C处的俯角为α，无人机沿水平线AF方向继续飞行40m至B处，测得正前方隧道出口D处的俯角为22°.线段AM的长为无人机距地面的垂直高度，点M，C，D在地面的正投影在同一条直线上，其中$\tan\alpha=3$，隧道高度CE=5m，ME=60m.
(1)求无人机的飞行高度AM；
(2)求隧道的长度CD.(参考数据：$\sin22^{\circ}\approx0.4$，$\cos22^{\circ}\approx0.9$，$\tan22^{\circ}\approx0.4$)

答案：
(1)延长DC交AM于点H,过点B作$BN\perp CD$,垂足为N.由题意可知,$\angle ACH=\alpha$,$\angle BDH=22°$,$AB=HN=40\ m$.在$Rt\triangle ACH$中,$\tan\angle ACH=\tan\alpha=\frac{AH}{HC}=3$,$HC=ME=60\ m$,$\therefore AH=BN=3HC=180\ m$.$\because HM=CE=5\ m$,$\therefore AM=AH+HM=185\ m$.
答:无人机的飞行高度AM为185 m.
(2)在$Rt\triangle BND$中,$\because\tan\angle BDN=\frac{BN}{DN}$,即$\tan22°=\frac{180}{DN}\approx0.4$,$\therefore DN\approx450\ m$.$\because CN=HC-HN=60-40=20(m)$,$\therefore CD=DN-CN\approx450-20=430(m)$.
答:隧道的长度CD约为430 m.