《2025年名校课堂九年级数学全一册湘教版广西专版》

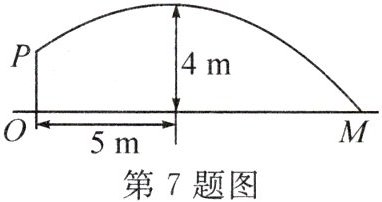
7. (2024·广西)如图，壮壮同学投掷实心球，出手(点$P$处)的高度$OP$是$\frac{7}{4}m$，出手后实心球沿一段抛物线运行，到达最高点时，与壮壮的水平距离是$5m$，高度是$4m$。若实心球落地点为$M$，则$OM = $$\frac{35}{3}$$m$。

答案： 7.$\frac{35}{3}$

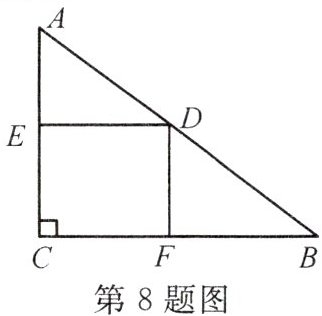
8. 如图，在$Rt\triangle ABC$中，$AC = 3cm$，$BC = 4cm$，四边形$CFDE$为矩形，其中$CF$，$CE$在两直角边上。设矩形的一边$CF = xcm$，当$x = $2时，矩形$CFDE$的面积最大，最大面积是$3\ cm^{2}$。

答案： 8.2 $3\ cm^{2}$

9. 新考向 真实情境 为迎接2025年元旦，学校准备开展“冬日情暖，喜迎元旦”活动，小星同学对会场进行装饰，如图1所示，他在会场的两墙$AB$，$CD$之间悬挂一条近似抛物线$y = ax^{2}-\frac{4}{5}x + 3$的彩带，如图2所示。已知墙$AB$与$CD$等高，且$AB$，$CD$之间的水平距离$BD$为8米。



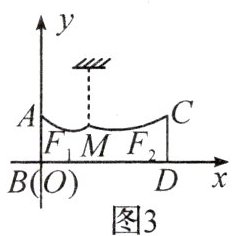
(1)如图2，两墙$AB$，$CD$的高度是3米，抛物线的顶点坐标为(4,1.4)；
(2)为了使彩带的造型美观，小星把彩带从点$M$处用一根细线吊在天花板上，如图3所示，使得点$M$到墙$AB$距离为3米，使抛物线$F_{1}$的最低点距墙$AB$的距离为2米，离地面2米，求点$M$到地面的距离。

答案： 9.解:
(1)3 (4,1.4)
(2)设抛物线的表达式为$y=a'(x-2)^{2}+2$,将点A(0,3)代入上式,得$3=a'(0-2)^{2}+2$,解得$a'=\frac{1}{4}$.$\therefore$抛物线的表达式为$y=\frac{1}{4}(x-2)^{2}+2$.当$x=3$时,$y=\frac{1}{4}(x-2)^{2}+2=2.25$.$\therefore$点M到地面的距离为2.25米.

10. 新考向 跨学科 综合与实践：
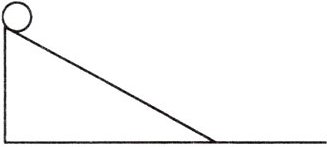
【问题背景】根据物理学知识可知，物体匀加（减）速运动时的路程$=$平均速度$\overline{v}×$时间$t$，$\overline{v}=\frac{v_{0}+v_{t}}{2}$。其中$v_{0}$是开始时的速度，$v_{t}$是$t$秒时的速度。
如图，钢球从斜面顶端由静止开始沿斜面滚下，速度每秒增加$1.5m/s$。
【问题理解】
（1）直接写出钢球在斜面滚动$t$秒时的速度$v_{t}$；
（2）求钢球在斜面滚动的距离$s(m)$关于滚动的时间$t(s)$的函数表达式；
【初步应用】
（3）如果斜面的长是$3m$，那么钢球从斜面顶端滚到底端需用多长时间？
【拓展探究】
（4）在（3）的条件下，钢球从斜面顶端滚到底端后，继续在水平地面上滚动，速度每秒减少$0.5m/s$，求钢球静止时在水平地面上滚动的路程。

答案： 10.解:
(1)钢球在斜面滚动t秒时的速度$v_{t}=1.5t$.
(2)由
(1)得$v_{t}=1.5t$,$\therefore \overline{v}=\frac{v_{0}+v_{t}}{2}=\frac{0+1.5t}{2}=\frac{3}{4}t$.$\therefore s=\overline{v}t=\frac{3}{4}t^{2}$.
(3)把$s=3$代入$s=\frac{3}{4}t^{2}$中,得$3=\frac{3}{4}t^{2}$,解得$t=2$或$t=-2$(不合题意,舍去).$\therefore$钢球从斜面顶端滚到底端需用2s.
(4)由题意,得钢球到底端时的速度$v=1.5× 2=3(m/s)$.$\therefore$记此时$v_{0}=3\ m/s$.$\because$速度每秒减少$0.5\ m/s$,$\therefore$钢球在水平地面上滚动t秒的速度$v_{t}=3-0.5t$.$\therefore$钢球在水平地面上的平均速度$\overline{v}=\frac{v_{0}+v_{t}}{2}=\frac{3+3-0.5t}{2}=-\frac{1}{4}t+3$.$\therefore$钢球在水平地面上滚动的距离$s=\overline{v}t=-\frac{1}{4}t^{2}+3t=-\frac{1}{4}(t-6)^{2}+9$.$\therefore$当$t=6$时,钢球滚动到最大距离,此时停止,距离为9m.
答:钢球静止时在水平地面上滚动的路程为9m.