《2025年名校课堂九年级数学全一册湘教版广西专版》

11. 下列函数：① $ y=2 x-1 $；② $ y=1-\sqrt{2} x^{2} $；③ $ y=3 x^{3}-2 x^{2} $；④ $ y=9 x^{2}-(3 x - 1)^{2} $；⑤ $ y=x^{2}+\frac{1}{x}+5 $；⑥ $ y=\frac{1}{2}(x - 1)(x + 4) $，其中二次函数有(B)

A.1 个
B.2 个
C.3 个
D.4 个

答案： 11.B

12. 在半径为 $ 4 \mathrm{~cm} $ 的圆中挖出一个半径为 $ x \mathrm{~cm} $($ 0＜x＜4 $)的圆，剩下的圆环的面积是 $ y \mathrm{~cm}^{2} $，则 $ y $ 与 $ x $ 的函数关系式为(D)

A.$ y=\pi x^{2}-4 $
B.$ y=\pi(2 - x)^{2} $
C.$ y=\pi(x^{2}+4) $
D.$ y=-\pi x^{2}+16 \pi $

答案： 12.D

13. 【易错】已知关于 $ x $ 的函数 $ y=(|m|-1) x^{2}+(m - 1) x + m + 1 $。
(1) 若这个函数是一次函数，则 $ m= $ ；-1
(2) 若这个函数是二次函数，则 $ m $ 的取值范围是 。m≠±1

答案： 13.
(1)-1
(2)m≠±1

14. 顺达旅行社为吸引游客到北帝山旅游区旅游，推出如下收费标准：
如果人数不超过 25 人，人均旅游费用为 1000 元。
如果人数超过 25 人，每超过 1 人，人均旅游费用降低 20 元。 
若某公司准备组织 $ x(x＞25) $ 名员工去北帝山旅游区旅游，公司需支付给顺达旅行社旅游费用 $ y $ 元，则 $ y $ 与 $ x $ 之间的函数表达式是 。y=-20x²+1500x

答案： 14.y=-20x²+1500x

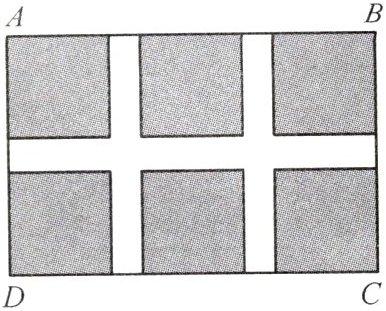
15. 新考向 模型观念 (教材九下 P4 习题 T3 变式) 如图所示，某小区计划在一个长为 $ 40 \mathrm{~m} $、宽为 $ 26 \mathrm{~m} $ 的矩形场地 $ ABCD $ 上修建三条宽均为 $ x \mathrm{~m} $ 的通路，使其中两条与 $ AB $ 垂直，另一条与 $ AB $ 平行，剩余部分种草，设剩余部分的面积为 $ y \mathrm{~m}^{2} $，求 $ y $ 关于 $ x $ 的函数表达式，并写出自变量的取值范围。

答案： 15.解:依题意,得y=(40-2x)(26-x)=2x²-92x+1040.由{40-2x＞0,26-x＞0,解得x＜20.又
∵x＞0,
∴自变量x的取值范围是0＜x＜20.
∴所求函数表达式为y=2x²-92x+1040(0＜x＜20).

16. 综合与实践
【问题背景】
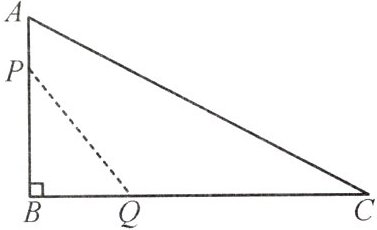
如图，在 $ \triangle ABC $ 中，$ \angle B=90^{\circ} $，$ AB=12 \mathrm{~cm} $，$ BC=24 \mathrm{~cm} $，动点 $ P $ 从点 $ A $ 开始沿边 $ AB $ 向 $ B $ 以 $ 2 \mathrm{~cm} / \mathrm{s} $ 的速度移动（不与点 $ B $ 重合），动点 $ Q $ 从点 $ B $ 开始沿边 $ BC $ 向点 $ C $ 以 $ 4 \mathrm{~cm} / \mathrm{s} $ 的速度移动（不与点 $ C $ 重合）。如果 $ P $，$ Q $ 两点分别从点 $ A $，$ B $ 同时出发，设运动的时间为 $ x \mathrm{~s} $，四边形 $ APQC $ 的面积为 $ y \mathrm{~cm}^{2} $。
【模型建立】
(1) 求 $ y $ 与 $ x $ 之间的函数关系式；
(2) 求自变量 $ x $ 的取值范围；
【问题解决】
(3) 四边形 $ APQC $ 的面积能否等于 $ 172 \mathrm{~cm}^{2} $？若能，求出运动的时间；若不能，说明理由。

答案： 16.解:
(1)由题意,得AP=2x cm,BQ=4x cm,则y=1/2BC·AB-1/2BQ·BP=1/2×24×12-1/2·4x·(12-2x),即y=4x²-24x+144.
(2)由题意,得{x＞0,2x＜12,4x＜24,
∴0＜x＜6.
(3)当y=172时,4x²-24x+144=172,解得x₁=7,x₂=-1(负值舍去).又
∵0＜x＜6,
∴四边形APQC的面积不能等于172 cm².