《2025年名校课堂九年级数学全一册湘教版广西专版》

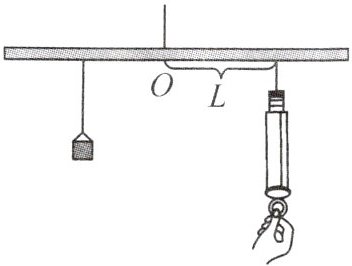
8. 新考向 跨学科 如图，取一根长100cm的匀质木杆，用细绳绑在木杆的中点O将其吊起来，在中点O的左侧，距离中点25cm处挂一个重9.8N的物体，在中点O右侧用一个弹簧秤向下拉，使木杆处于水平状态(杠杆平衡时，动力×动力臂=阻力×阻力臂).若弹簧秤与中点O的距离为L(cm)，弹簧秤的示数为F(N)，则当F=24.5N时，L的值为10 cm.

答案： 8.10 cm

9. 【问题情境】
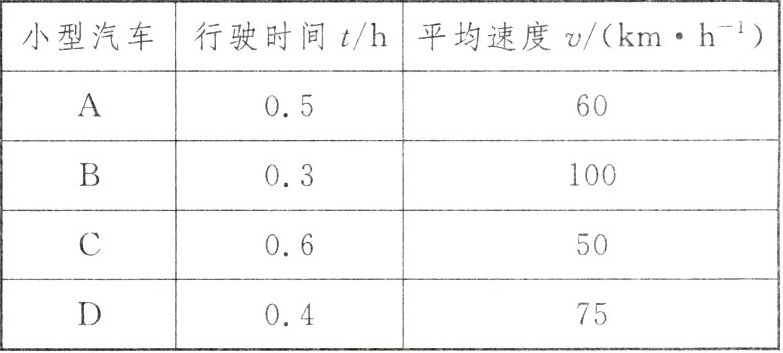
区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小聪搜集了某路段测速区间内若干小型汽车行驶的平均速度v(km/h)与行驶时间t(h)的数据如下表.
【建立模型】
(1)根据调查数据可知，该路段测速区间内小型汽车平均速度v(km/h)是行驶时间t(h)的函数.求v(km/h)与t(h)之间的函数关系式；

【问题解决】
(2)若某辆小汽车通过该测速区间的行驶时间为50分钟，求它的平均速度；
(3)已知该测速区间限速80km/h，小汽车通过该测速区间时，行驶时间应控制在怎样的范围内?

答案： 解:
(1)由表格可知$vt=30$,$\therefore v$(km/h)与$t$(h)之间的函数关系式为$v=\frac {30}{t}$.
(2)50分钟$=\frac {5}{6}$小时,当$t=\frac {5}{6}$时,$v=\frac {30}{\frac {5}{6}}=36$.
答:它的平均速度是36 km/h.
(3)根据题意,得$\frac {30}{t}\leqslant80$,解得$t\geqslant\frac {3}{8}$.$\frac {3}{8}$小时=22.5分钟.
答:行驶时间应不少于22.5分钟.

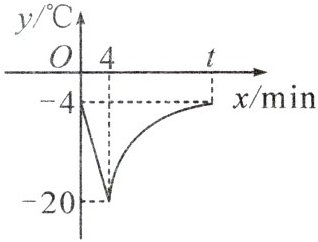
10. 如图，这是某型号冷柜循环制冷过程中温度变化的部分示意图.该冷柜的工作过程是：当冷柜温度达到-4℃时制冷开始，温度开始逐渐下降，当温度下降到-20℃时制冷停止，温度开始逐渐上升，当温度上升到-4℃时，制冷再次开始……按照以上方式循环工作.通过分析发现，当0≤x＜4时，温度y(℃)是时间x(min)的一次函数；当4≤x＜t时，温度y(℃)是时间x(min)的反比例函数.
(1)求t的值；
(2)当前冷柜的温度为-10℃，经过多长时间温度下降到-20℃?

答案： 解:
(1)设反比例函数的表达式为$y=\frac {k}{x}$.把$(4,-20)$代入,得$-20=\frac {k}{4}$.$\therefore k=-80$.$\therefore y=\frac {-80}{x}$.当$y=-4$时,$-4=\frac {-80}{t}$,$\therefore t=20$.
(2)设一次函数的表达式为$y=mx-4$.把$(4,-20)$代入,得$-20=4m-4$,解得$m=-4$.$\therefore y=-4x-4$.分两种情况讨论:①在温度下降过程中,$-10=-4x-4$,解得$x=1.5$.$\therefore 4-1.5=2.5$(min).此时经过2.5 min温度下降到$-20^{\circ }C$.②在温度上升过程中,$-10=\frac {-80}{x}$,解得$x=8$.$\therefore 20-8+4=16$(min).此时经过16 min温度下降到$-20^{\circ }C$.综上所述,经过2.5 min或16 min温度下降到$-20^{\circ }C$.