《2025年名校课堂九年级数学全一册湘教版广西专版》

10. (2024·广西)如图，在边长为 $5$ 的正方形 $ABCD$ 中，$E,F,G,H$ 分别为各边的中点，连接 $AG,BH,CE,DF$，交点分别为 $M,N,P,Q$，那么四边形 $MNPQ$ 的面积为(C)

A.$1$
B.$2$
C.$5$
D.$10$

答案： C

11. (2024·贵港覃塘区期中)如图，在 $\triangle ABC$ 中，$AD$ 是角平分线，点 $E,F$ 分别在线段 $AB,AD$ 上，且 $\angle EFD = \angle BDF$.
(1) 求证：$\triangle AFE \backsim \triangle ADC$；
(2) 若 $\frac{AE}{AC}=\frac{4}{5}$，$\frac{AE}{BE}=2$，且 $\angle AFE = \angle C$，探索 $BE$ 和 $DF$ 之间的数量关系.

答案：
(1)证明:
∵AD为$\angle BAC$的平分线,$\therefore \angle FAE=\angle DAC$.$\because \angle EFD=\angle BDF$,$\therefore 180^{\circ}-\angle EFD=180^{\circ}-\angle BDF$.$\therefore \angle AFE=\angle ADC$.$\therefore \triangle AFE\backsim \triangle ADC$.
(2)由
(1)得,$\triangle AFE\backsim \triangle ADC$.$\therefore \frac{AF}{AD}=\frac{AE}{AC}=\frac{4}{5}$,$\angle AEF=\angle C$.$\therefore \frac{AF}{DF}=4$.$\therefore AF=4DF$.$\because \angle AFE=\angle C$,$\therefore \angle AEF=\angle AFE$.$\therefore AE=AF$.$\because \frac{AE}{BE}=2$,$\therefore \frac{AF}{BE}=\frac{AE}{BE}=2$.$\therefore AF=2BE$.$\therefore 2BE=4DF$.$\therefore BE=2DF$.

12. 新考向 真实情境(2024·贵港覃塘区期中)如图所示的为步枪在瞄准时的示意图，$AB // CD$，从眼睛 $O$ 到准星的距离 $OE$ 为 $80 cm$，到目标 $F$ 的距离 $OF$ 为 $200 m$，步枪上准星的宽度 $AB$ 为 $2 mm$. 若射击时，由于抖动导致视线偏离了准星上 $E$ 点 $1 mm$，则目标偏离的距离为(A)

A.$25 cm$
B.$50 cm$
C.$75 cm$
D.$100 cm$

答案： A

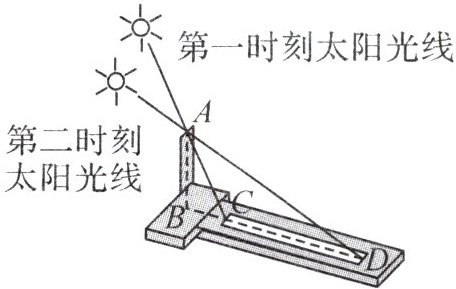
13. 新考向 传统文化(2024·广西模拟)土圭之法是指在平台中央竖立一根八尺长的杆子，观察杆子的日影长度. 古代的人们发现，夏至时日影最短，冬至时日影最长，这样通过日影的长度得到夏至和冬至，确定了四季. 如图，利用土圭之法记录了两个时刻杆的影长，发现第一时刻太阳光线与杆的夹角 $\angle BAC$ 和第二时刻太阳光线与地面的夹角 $\angle ADB$ 相等，测得第一时刻的影长 $BC$ 为 $1.6$ 尺，则第二时刻的影长 $BD$ 为40尺.

答案： 40

14. 新考向 跨学科(2023·南宁民族中学期中)【学科融合】如图 $1$，在反射现象中，反射光线、入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角 $r$ 等于入射角 $i$. 这就是光的反射定律.
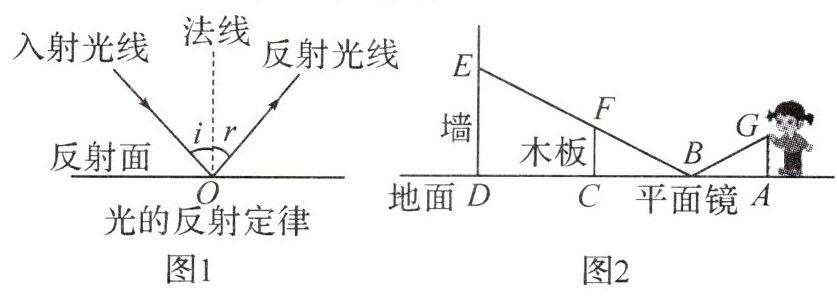
【问题解决】如图 $2$，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜，手电筒的灯泡在点 $G$ 处，手电筒的光从平面镜上点 $B$ 处反射后，恰好经过木板的边缘点 $F$，落在墙上的点 $E$ 处，点 $E$ 到地面的高度 $DE = 3.5 m$，点 $F$ 到地面的高度 $CF = 1.5 m$，灯泡到木板的水平距离 $AC = 5.4 m$，木板到墙的水平距离 $CD = 4 m$. 图中点 $A,B,C,D$ 在同一条直线上.
(1) 求 $BC$ 的长；
(2) 求灯泡到地面的高度 $AG$.

答案：
(1)由题意,得$FC// DE$,则$\triangle BFC\backsim \triangle BED$.$\therefore \frac{BC}{BD}=\frac{FC}{DE}$,即$\frac{BC}{BC+4}=\frac{1.5}{3.5}$,解得$BC=3$.$\therefore BC$的长为$3\ m$.
(2)$\because AC=5.4\ m$,$\therefore AB=AC-BC=5.4-3=2.4(m)$.$\because$光在镜面反射中的反射角等于入射角,$\therefore \angle FBC=\angle GBA$.又$\because \angle FCB=\angle GAB$,$\therefore \triangle BGA\backsim \triangle BFC$.$\therefore \frac{AG}{CF}=\frac{AB}{CB}$,即$\frac{AG}{1.5}=\frac{2.4}{3}$,解得$AG=1.2$.$\therefore$灯泡到地面的高度$AG$为$1.2\ m$.