第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
11. (2022·贵港)如图,直线 $ AB $ 与反比例函数 $ y = \frac{k}{x}(k > 0,x > 0) $ 的图象相交于点 $ A $ 和点 $ C(3,2) $,与 $ x $ 轴的正半轴相交于点 $ B $.
(1)求 $ k $ 的值;
(2)连接 $ OA,OC $,若点 $ C $ 为线段 $ AB $ 的中点,求 $ \triangle AOC $ 的面积.
 ]
]
(1)求 $ k $ 的值;
(2)连接 $ OA,OC $,若点 $ C $ 为线段 $ AB $ 的中点,求 $ \triangle AOC $ 的面积.
 ]
]
答案:
11.解:
(1)
∵点C(3,2)在反比例函数y=k/x的图象上,
∴k/3=2,解得k=6.
(2)
∵点C(3,2)是线段AB的中点,
∴易证点A的纵坐标为4.
∴点A的横坐标为6/4=3/2.
∴点A的坐标为(3/2,4).设直线AC的表达式为y=ax+b,则{3/2 a+b=4,3a+b=2,解得{a=-4/3,b=6.
∴直线AC的表达式为y=-4/3 x+6.
∵当y=0时,x=9/2,
∴OB=9/2.
∴S△AOC=1/2 S△AOB=1/2×1/2×9/2×4=9/2.
(1)
∵点C(3,2)在反比例函数y=k/x的图象上,
∴k/3=2,解得k=6.
(2)
∵点C(3,2)是线段AB的中点,
∴易证点A的纵坐标为4.
∴点A的横坐标为6/4=3/2.
∴点A的坐标为(3/2,4).设直线AC的表达式为y=ax+b,则{3/2 a+b=4,3a+b=2,解得{a=-4/3,b=6.
∴直线AC的表达式为y=-4/3 x+6.
∵当y=0时,x=9/2,
∴OB=9/2.
∴S△AOC=1/2 S△AOB=1/2×1/2×9/2×4=9/2.
12. 新考向 真实情境 (2024·贵港港南区模拟)图 1 是一盏亮度可调节的台灯,通过调节总电阻 $ R $ 来控制电流 $ I $ 实现灯光亮度的变化.电流 $ I(A) $ 与电阻 $ R(\Omega) $ 之间的函数关系如图 2 所示.下列结论正确的是 (

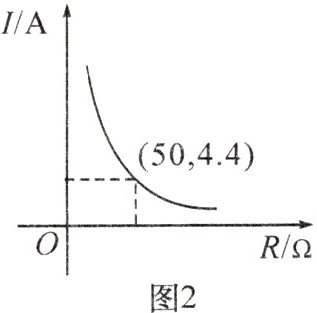
A.$ I = \frac{200}{R} $
B.当 $ I > 10 $ 时, $ R > 22 $
C.当 $ I = 5 $ 时, $ R = 40 $
D.当 $ I > 2 $ 时, $ 0 < R < 110 $
D
)

A.$ I = \frac{200}{R} $
B.当 $ I > 10 $ 时, $ R > 22 $
C.当 $ I = 5 $ 时, $ R = 40 $
D.当 $ I > 2 $ 时, $ 0 < R < 110 $
答案:
D
13. (2023·贵港港北区模拟)如图,这是某公园“水上滑梯”的侧面图,其中 $ BC $ 段可看成是一段双曲线,建立如图所示的平面直角坐标系.已知矩形 $ AOEB $ 为向上攀爬的梯子, $ OA = 5 $ 米,进口 $ AB // OD $,且 $ AB = 2 $ 米,出口 $ C $ 点距水面的距离 $ CD $ 为 1 米,则 $ B,C $ 之间的水平距离 $ DE $ 的长度为 (
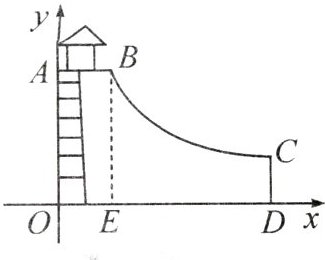
A.5 米
B.6 米
C.7 米
D.8 米
D
)
A.5 米
B.6 米
C.7 米
D.8 米
答案:
D
14. 新考向 跨学科 (2024·南宁银海三雅模拟)寓言故事:青年用木柴烧水时,由于木柴不足,水没有烧开,重新找木柴的时间水已变凉,而新找的木柴也不够将水重新烧开,很是气馁.路过的智者提醒他,木柴不够,可以将水倒掉一部分.青年听后,茅塞顿开,把水烧开了.智者的话蕴含一定道理,根据物理学公式 $ Q = cm\Delta t $ ( $ Q $ 表示寓言故事中水吸收的总热量, $ c $ 表示水的比热容,为常数, $ m $ 表示水的质量, $ \Delta t $ 表示水的温差),得 $ \Delta t = \frac{Q}{cm} $.智者的话可解释为:当木柴质量确定时,提供给水吸收的总热量 $ Q $ 随之确定, $ \frac{Q}{c} $ 为定值,水上升的温度 $ \Delta t(^{\circ}C) $ 与水的质量 $ m(kg) $ 成反比例.
(1)若现有木柴可以将 $ 3kg $ 温度为 $ 25^{\circ}C $ 的水加热到 $ 75^{\circ}C $,请求出这种情形下 $ \frac{Q}{c} $ 的值及 $ \Delta t $ 关于 $ m $ 的反比例函数的表达式;
(2)在(1)的情形下,现有的木柴可将多少千克温度为 $ 25^{\circ}C $ 的水加热到 $ 100^{\circ}C $?
(1)若现有木柴可以将 $ 3kg $ 温度为 $ 25^{\circ}C $ 的水加热到 $ 75^{\circ}C $,请求出这种情形下 $ \frac{Q}{c} $ 的值及 $ \Delta t $ 关于 $ m $ 的反比例函数的表达式;
(2)在(1)的情形下,现有的木柴可将多少千克温度为 $ 25^{\circ}C $ 的水加热到 $ 100^{\circ}C $?
答案:
14.解:
(1)根据题意,得Δt=Q/(cm).
∵将3 kg温度为25℃的水加热到75℃,
∴m=3 kg,Δt=75-25=50(℃).
∴50=Q/(3c).
∴Q/c=150.
∴Δt=150/m.
∴Q/c的值为150,Δt关于m的反比例函数的表达式为Δt=150/m.
(2)
∵将25℃的水加热到100℃,
∴Δt=100-25=75(℃).
∴75=150/m,解得m=2.
∴现有的木柴可将2 kg温度为25℃的水加热到100℃.
(1)根据题意,得Δt=Q/(cm).
∵将3 kg温度为25℃的水加热到75℃,
∴m=3 kg,Δt=75-25=50(℃).
∴50=Q/(3c).
∴Q/c=150.
∴Δt=150/m.
∴Q/c的值为150,Δt关于m的反比例函数的表达式为Δt=150/m.
(2)
∵将25℃的水加热到100℃,
∴Δt=100-25=75(℃).
∴75=150/m,解得m=2.
∴现有的木柴可将2 kg温度为25℃的水加热到100℃.
查看更多完整答案,请扫码查看


