第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
1.(教材P30练习T2·变式)如图,在△ABC和△ADC中,AB= AD,添加下列哪个条件,不能使△ABC≌△ADC的是(
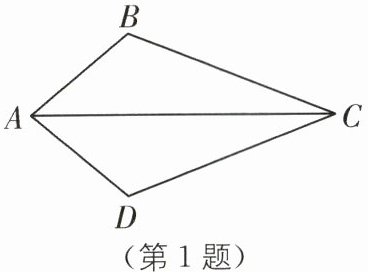
A.∠BAC= ∠DAC
B.∠BCA= ∠DCA
C.∠ABC= ∠ADC= 90°
D.BC= DC
B
).
A.∠BAC= ∠DAC
B.∠BCA= ∠DCA
C.∠ABC= ∠ADC= 90°
D.BC= DC
答案:
B
2.(2025·宿迁宿城区期中)如图,点F,B,E,C在同一条直线上,△ABC≌△DEF,若∠A= 24°,∠F= 26°,则∠DEC的度数为(

A.50°
B.60°
C.70°
D.80°
A
).
A.50°
B.60°
C.70°
D.80°
答案:
A
3.(新情境)自行车模型如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的(

A.全等形
B.稳定性
C.灵活性
D.对称性
B
).
A.全等形
B.稳定性
C.灵活性
D.对称性
答案:
B
4.(变式提优B卷T1)(2025·盐城盐都区期中)根据下列已知条件,能画出唯一的△ABC的是(
A.AB= 5,AC= 4,BC= 1
B.AB= 5,AC= 4,∠B= 60°
C.∠A= 30°,∠B= 60°,∠C= 90°
D.∠A= 30°,∠B= 60°,AB= 5
D
).A.AB= 5,AC= 4,BC= 1
B.AB= 5,AC= 4,∠B= 60°
C.∠A= 30°,∠B= 60°,∠C= 90°
D.∠A= 30°,∠B= 60°,AB= 5
答案:
D
5.如图,在6×5的网格中,点A,B在格点上,点C也在格点上,且△ABC是等腰三角形,则符合条件的点C的个数是( ).
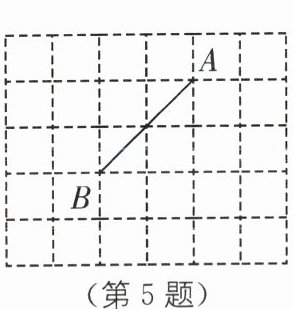
A.6
B.7
C.8
D.9

A.6
B.7
C.8
D.9
答案:
5.C [解析]如图,

分三种情况:分别以A,B,C为顶点画等腰三角形。当BA=BC时,以点B为圆心,以BA长为半径作圆,交正方形网格的格点于点C₁,C₂;当AB=AC时,以点A为圆心,以AB长为半径作圆,交正方形网格的格点于点C₃;当CA=CB时,作AB的垂直平分线,交正方形网格的格点于点C₄,C₅,C₆,C₇,C₈。
综上所述,要使△ABC是等腰三角形,符合条件的点C的个数为8。故选C。
5.C [解析]如图,

分三种情况:分别以A,B,C为顶点画等腰三角形。当BA=BC时,以点B为圆心,以BA长为半径作圆,交正方形网格的格点于点C₁,C₂;当AB=AC时,以点A为圆心,以AB长为半径作圆,交正方形网格的格点于点C₃;当CA=CB时,作AB的垂直平分线,交正方形网格的格点于点C₄,C₅,C₆,C₇,C₈。
综上所述,要使△ABC是等腰三角形,符合条件的点C的个数为8。故选C。
6.(2023·河北中考)四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为(
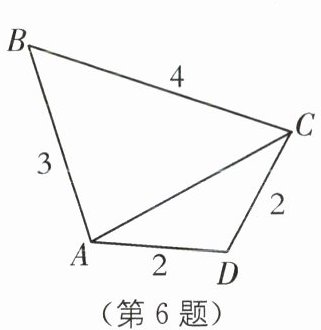
A.2
B.3
C.4
D.5
B
).
A.2
B.3
C.4
D.5
答案:
B
7.(变式提优B卷T8)(2024·南通海安期中)如图,在△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE//BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE= BD+CE;③BC= BD+CE;④△ADE的周长= AB+AC;⑤BF= CF.其中正确的有(
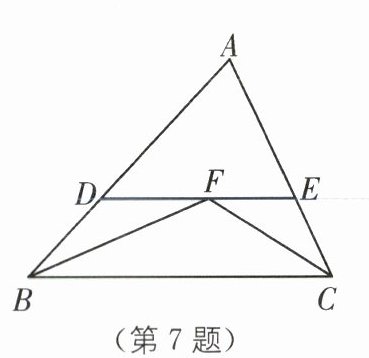
A.①②③
B.①②④
C.①②④⑤
D.②④⑤
B
).
A.①②③
B.①②④
C.①②④⑤
D.②④⑤
答案:
7.B [解析]
∵DE//BC,
∴∠DFB=∠FBC,∠EFC=∠FCB。
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DBF,∠FCE=∠FCB,
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DF=DB,FE=EC,
∴DE=DF+FE=DB+EC,
∴△ADE的周长=AD+AE+DE=AD+AE+DB+EC=AB+AC。综上所述,①②④正确,③⑤无法得到。故选B。
∵DE//BC,
∴∠DFB=∠FBC,∠EFC=∠FCB。
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DBF,∠FCE=∠FCB,
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DF=DB,FE=EC,
∴DE=DF+FE=DB+EC,
∴△ADE的周长=AD+AE+DE=AD+AE+DB+EC=AB+AC。综上所述,①②④正确,③⑤无法得到。故选B。
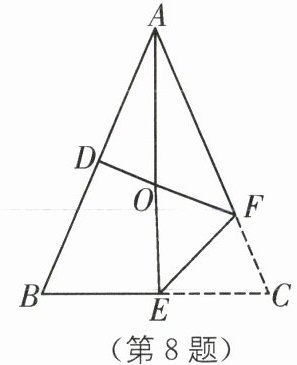
8.如图,在△ABC中,AB= AC,∠BAC= 46°,∠BAC的平分线与AB的垂直平分线OD交于点O,点E在BC上,点F在AC上,连接EF.将∠C沿EF折叠,当点C与点O恰好重合时,∠OEC的度数为( ).
A.90°
B.92°
C.95°
D.98°

A.90°
B.92°
C.95°
D.98°
答案:
8.B [解析]如图,连接BO,CO。

∵∠BAC=46°,AO平分∠BAC,
∴∠OAB=∠OAC=23°。
∵OD是AB的垂直平分线,
∴OA=OB,
∴∠OAB=∠OBA=23°。
∵AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180° - ∠BAC)=67°,
∴∠OBC=∠ABC - ∠OBA=67° - 23°=44°。
∵AB=AC,∠OAB=∠OAC,AO=AO,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=44°。
由折叠可知,EO=EC,
∴∠EOC=∠ECO=44°,
∴∠OEC=180° - ∠EOC - ∠ECO=180° - 2×44°=92°。
故选B。
8.B [解析]如图,连接BO,CO。

∵∠BAC=46°,AO平分∠BAC,
∴∠OAB=∠OAC=23°。
∵OD是AB的垂直平分线,
∴OA=OB,
∴∠OAB=∠OBA=23°。
∵AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180° - ∠BAC)=67°,
∴∠OBC=∠ABC - ∠OBA=67° - 23°=44°。
∵AB=AC,∠OAB=∠OAC,AO=AO,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=44°。
由折叠可知,EO=EC,
∴∠EOC=∠ECO=44°,
∴∠OEC=180° - ∠EOC - ∠ECO=180° - 2×44°=92°。
故选B。
查看更多完整答案,请扫码查看


