第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
1. (教材P88练习T1·变式 (2025·如东期末改编)已知,Rt△ABC的两条直角边AC,BC的长分别为4,3,则它的斜边AB上的高为(
A.3
B.4
C.5
D.$\frac{12}{5}$
D
).A.3
B.4
C.5
D.$\frac{12}{5}$
答案:
D
2. 传统文化 赵爽弦图 (2024·南通中考)"赵爽弦图"巧妙利用面积关系证明了勾股定理.如图所示的"赵爽弦图"是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为5,$(m+n)^2= 21$,则大正方形面积为(
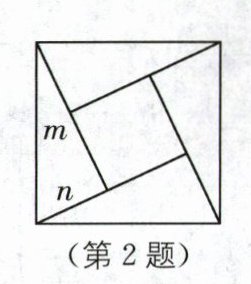
A.12
B.13
C.14
D.15
B
).
A.12
B.13
C.14
D.15
答案:
B
3. (2025·四川成都锦江区期末)图中的四边形均为正方形,三角形为直角三角形,最大的正方形的边长为7 cm,则图中A,B两个正方形的面积之和为(
$A.28 cm^2$
$B.42 cm^2$
$C.49 cm^2$
$D.63 cm^2$
C
).$A.28 cm^2$
$B.42 cm^2$
$C.49 cm^2$
$D.63 cm^2$
答案:
C
4. (2025·徐州期中)下列由三条线段a,b,c构成的三角形$:①∠A+∠B= ∠C;②a= 3k,b= 4k,c= 5k(k>0);③∠A:∠B:∠C= 3:4:5;④a= m^2+1,b= m^2-1,c= 2m(m$为大于1的整数).其中能构成直角三角形的是(
A.①④
B.①②④
C.②③④
D.①②③
B
).A.①④
B.①②④
C.②③④
D.①②③
答案:
B [解析]①
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C+∠C=180°,
∴∠C=90°,
∴能构成直角三角形;②
∵a²+b²=(3k)²+(4k)²=25k²,c²=(5k)²=25k²,
∴a²+b²=c²,
∴能构成直角三角形;③
∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴∠C=180°×$\frac{5}{3 + 4 + 5}$=75°,
∴不能构成直角三角形;④
∵a²=(m²+1)²=m⁴+2m²+1,b²+c²=(m² - 1)²+(2m)²=m⁴ - 2m²+1+4m²=m⁴+2m²+1,
∴a²=b²+c²,
∴能构成直角三角形,所以,能构成直角三角形的是①②④.故选B.
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴∠C+∠C=180°,
∴∠C=90°,
∴能构成直角三角形;②
∵a²+b²=(3k)²+(4k)²=25k²,c²=(5k)²=25k²,
∴a²+b²=c²,
∴能构成直角三角形;③
∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,
∴∠C=180°×$\frac{5}{3 + 4 + 5}$=75°,
∴不能构成直角三角形;④
∵a²=(m²+1)²=m⁴+2m²+1,b²+c²=(m² - 1)²+(2m)²=m⁴ - 2m²+1+4m²=m⁴+2m²+1,
∴a²=b²+c²,
∴能构成直角三角形,所以,能构成直角三角形的是①②④.故选B.
5. 传统文化 《周髀算经》 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图(1),以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图(2)的方式放置在最大正方形内.若图(2)中阴影部分的面积为4,且AB+AC= 7,则下列数值中可为BC长的是(
A.5
B.9
C.$\sqrt{29}$
D.$\sqrt{37}$
A
).A.5
B.9
C.$\sqrt{29}$
D.$\sqrt{37}$
答案:
A
6. 如图,在△ABC中,∠ABC= 90°,AB= 8,BC= 12,D为AC边上的一个动点,连接BD,E为BD上的一个动点,连接AE,CE,当∠ABD= ∠BCE时,线段AE的最小值是( ).
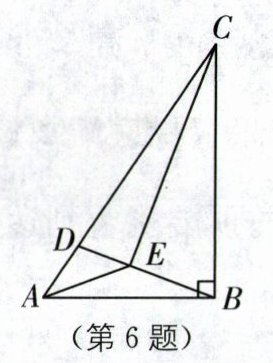
A.3
B.4
C.5
D.6

A.3
B.4
C.5
D.6
答案:
B [解析]如图,取BC的中点T,连接AT,ET.
∵∠ABC=90°,
∴∠ABD+∠CBD=90°.

∵∠ABD=∠BCE,
∴∠CBD+∠BCE=90°,
∴∠CEB=90°.
∵CT=TB=6,
∴ET=$\frac{1}{2}$BC=6,AT²=AB²+BT²=8²+6²=100,即AT=10.
∵AE≥AT - ET,
∴AE≥4,
∴AE的最小值为4.故选B.
归纳总结 本题考查直角三角形斜边中线的性质、勾股定理等知识,解题的关键是求出AT,ET的长.
B [解析]如图,取BC的中点T,连接AT,ET.
∵∠ABC=90°,
∴∠ABD+∠CBD=90°.

∵∠ABD=∠BCE,
∴∠CBD+∠BCE=90°,
∴∠CEB=90°.
∵CT=TB=6,
∴ET=$\frac{1}{2}$BC=6,AT²=AB²+BT²=8²+6²=100,即AT=10.
∵AE≥AT - ET,
∴AE≥4,
∴AE的最小值为4.故选B.
归纳总结 本题考查直角三角形斜边中线的性质、勾股定理等知识,解题的关键是求出AT,ET的长.
7. (2024·南京秦淮区期中)三角形的三边长为a,b,c,且满足等式$(a+b)^2-c^2= 2ab$,则此三角形是
直角
(填“直角”“锐角”或“钝角”)三角形.
答案:
直角
8. 如图,在△ABC中,∠C= 90°,若c= 2,则$a^2+b^2+c^2=$
8
.
答案:
8
查看更多完整答案,请扫码查看


