第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
9.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AC= 3 km,BC= 4 km,则M,C两点间的距离为
2.5
km.
答案:
2.5 [解析]
∵公路 AC,BC 互相垂直,
∴∠ACB=90°.
∵AC=3km,BC=4km,
∴由勾股定理,得 AB²=AC²+BC²=3²+4²=25,
∴AB=5km.
∵点 M 为 AB 的中点,
∴CM=1/2 AB=2.5km,即 M,C 两点间的距离为 2.5km.
∵公路 AC,BC 互相垂直,
∴∠ACB=90°.
∵AC=3km,BC=4km,
∴由勾股定理,得 AB²=AC²+BC²=3²+4²=25,
∴AB=5km.
∵点 M 为 AB 的中点,
∴CM=1/2 AB=2.5km,即 M,C 两点间的距离为 2.5km.
10.(2025·无锡锡山区期中)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合二寸,问门广几何?题目的大致意思是:如图(1)、(2)(图(2)为图(1)的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都是1尺(1尺= 10寸),则AB长是几寸?若设图中单扇门的宽AD= x寸,则可列方程为______.______
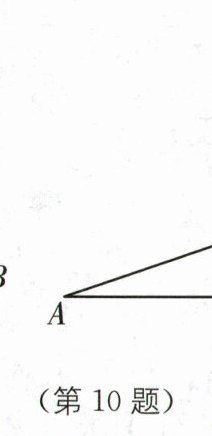

(x - 1)²+10²=x²
答案:
(x - 1)²+10²=x² [解析]取 AB 的中点 O,过点 D 作 DE⊥AB 于 E,如图所示.由题意,得 OA=OB=AD=BC.设 OA=OB=AD=BC=x 寸,则 AB=2x 寸,DE=10 寸,OE=1/2 CD=1 寸,
∴AE=(x - 1)寸.在 Rt△ADE 中,AE²+DE²=AD²,即(x - 1)²+10²=x².
∴AE=(x - 1)寸.在 Rt△ADE 中,AE²+DE²=AD²,即(x - 1)²+10²=x².
11. 教材P105复习题T5·变式 将一根长为120 cm的木棒放入长、宽分别是120 cm、40 cm、30 cm的箱子中(如图),能放进去吗?答:
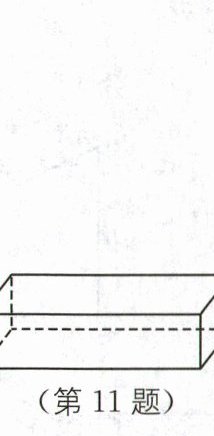
能
(填“能”或“不能”).
答案:
能 [解析]如图,连接 AC,AE,由题意,得 AB=30cm,CE=120cm,BC=40cm,∠ABC=90°,∠ACE=90°.在 Rt△ABC 中,由勾股定理,得 AC²=AB²+BC²=30²+40²=2500,在 Rt△ACE 中,由勾股定理,得 AE²=AC²+CE²=2500+14400=16900,
∴AE=130cm.
∵120cm<130cm,
∴能放进去.
∴AE=130cm.
∵120cm<130cm,
∴能放进去.
12.(10分)传统文化 《算法统宗》 (2025·湖南衡阳期末)明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》: “平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC= 1尺),将它往前推进两步(古代5尺为一步,EB= 10尺),此时踏板升高离地五尺(BD= 5尺),求秋千绳索(OA或OB)的长度.
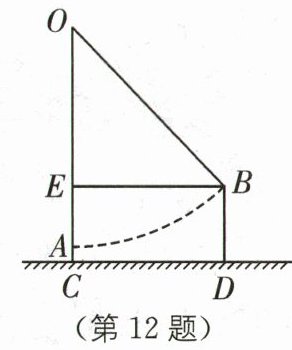

答案:
设 OA=OB=x 尺.
∵EC=BD=5 尺,AC=1 尺,
∴EA=EC - AC=5 - 1=4(尺),OE=OA - AE=(x - 4)尺.在 Rt△OEB 中,OE=(x - 4)尺,OB=x 尺,EB=10 尺,根据勾股定理,得 x²=(x - 4)²+10²,整理,得 8x=116,解得 x=14.5.故秋千绳索的长度为 14.5 尺.
∵EC=BD=5 尺,AC=1 尺,
∴EA=EC - AC=5 - 1=4(尺),OE=OA - AE=(x - 4)尺.在 Rt△OEB 中,OE=(x - 4)尺,OB=x 尺,EB=10 尺,根据勾股定理,得 x²=(x - 4)²+10²,整理,得 8x=116,解得 x=14.5.故秋千绳索的长度为 14.5 尺.
13.(10分)新情境 放风筝 (2025·连云港灌南期中)长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所.某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,如图所示,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE.
(2)如果小明想让风筝沿CD方向下降12米,那么他应该往回收线多少米?
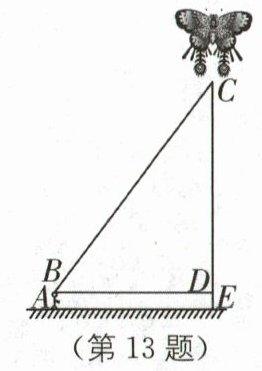
(1)求风筝的垂直高度CE.
(2)如果小明想让风筝沿CD方向下降12米,那么他应该往回收线多少米?

答案:
(1)在 Rt△CDB 中,由勾股定理,得 CD²=BC² - BD²=25² - 15²=400,所以 CD=20(负值舍去),所以 CE=CD+DE=20+1.6=21.6(米).故风筝的高度 CE 为 21.6 米.
(2)如图,设风筝下降至点 M 处,则 CM=12 米,
∴DM=8 米,
∴BM²=DM²+BD²=8²+15²=289,
∴BM=17 米,
∴BC - BM=25 - 17=8(米),
∴他应该往回收线 8 米.
(1)在 Rt△CDB 中,由勾股定理,得 CD²=BC² - BD²=25² - 15²=400,所以 CD=20(负值舍去),所以 CE=CD+DE=20+1.6=21.6(米).故风筝的高度 CE 为 21.6 米.
(2)如图,设风筝下降至点 M 处,则 CM=12 米,
∴DM=8 米,
∴BM²=DM²+BD²=8²+15²=289,
∴BM=17 米,
∴BC - BM=25 - 17=8(米),
∴他应该往回收线 8 米.
查看更多完整答案,请扫码查看


