《2025年实验班提优大考卷八年级数学上册苏科版》

8.中考新考法 规律探究 (2025·镇江期中)有一个面积为1的正方形,经过一次"生长"后,在它的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次"生长"后,变成了如图所示的形状,如果继续"生长"下去,它将变得"枝繁叶茂",那么"生长"了2022次后形成的图形中所有正方形的面积和是( ).

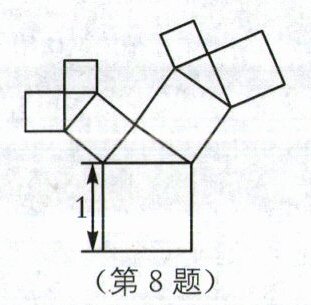
A.1
B.2021
C.2022
D.2023

答案：
D [解析]如图，由题意，得正方形A的面积为1,
由勾股定理，得正方形B的面积+正方形C的面积=1,
∴"生长"了1次后形成的图形中所有正方形的面积和为2,
同理，可得"生长"了2次后形成的图形中所有正方形的面积和为3，
∴"生长"了3次后形成的图形中所有正方形的面积和为4,
…,
∴"生长"了2022次后形成的图形中所有正方形的面积和为2023.故选D.

9.(2025·甘肃庆阳期末)如图,小明在池塘一侧选取了一点 O,测得$OA= 16\ m$,$OB= 12\ m$,则池塘两岸 A,B 间的距离可以是______m.(写出一个即可)

26

答案： 26(答案不唯一)

10.(2025·常州期中)若一个三角形的三边长分别为5,12,13,则此三角形的最长边上的高为$\frac{60}{13}$.

答案： $\frac{60}{13}$

11.新情境 制作简易模型 为了庆祝神舟二十号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足$\triangle ABD\cong\triangle ACE$,点 B 和点 C 是对应顶点,若$AB= $$8\ cm$,$AD= 3\ cm$,则$DC= $5cm.

答案： 5

12.如图,在$\triangle ABC$中,$AB= AC$,点 D 在 BC 上,点 F 在 AC 上,$DE\perp AB$于点 E,$BE= CD$,$BD= CF$,若$\angle B= 55^{\circ}$,则$\angle EDF$的度数为______55°.

答案： 55°

13.(广东深圳中学自主招生)一个三角形三边长分别为$5k$,$12k$,$13k$,面积$S\leq900$,满足情况的正整数$k$有5个.

答案： 5 [解析]由题意,得(5k)²+(12k)²=(13k)²,
∴该三角形为直角三角形，且两直角边的长分别是5k，12k,
∴S=$\frac{1}{2}$×5k×12k=30k².
∵S≤900,
∴30k²≤900,
∴k²≤30.
又k为正整数，
∴k=1,2,3,4,5,
∴满足情况的正整数k有5个.

14.(2025·无锡期末)如图,以$Rt\triangle ACB$的两边 AB,BC 为边向外所作正方形的面积分别是$26\ cm^2$,$10\ cm^2$,则以另一边 AC 为直径向外作半圆的面积为2π$cm^2$.

答案： 2π [解析]
∵以Rt△ACB的两边AB,BC为边向外所作正方形的面积分别是26cm²,10cm²，AC²=AB²-BC²,
∴AC²=26-10=16,
∴以另一边AC为直径向外作半圆的面积为$\frac{1}{2}$π×($\frac{AC}{2}$)²=$\frac{1}{2}$π×$\frac{16}{4}$=2π(cm²).
注意求面积需代入半径，勿代错
方法诠释本题考查勾股定理以及正方形和圆的面积，牢记"在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方"是解题的关键.

15.如图,线段 AB,BC 的垂直平分线$l_1$,$l_2$相交于点 O.若$\angle1= 39^{\circ}$,则$\angle AOC= $78°.

答案： 78°

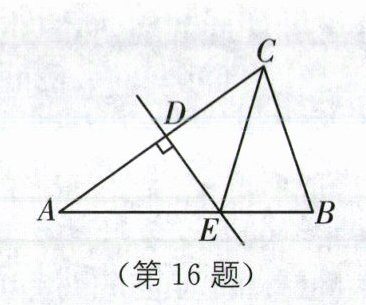
16.(2025·扬州仪征期中)如图,在$\triangle ABC$中,AC 的垂直平分线分别交边 AC,AB 于点 D 和点 E,连接CE.若$BC= 4$,$AB= 6$,则$\triangle CBE$周长为______10.

答案： 10

17.分类讨论思想 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为______.

答案：
36°或45° [解析]分两种情况讨论:
①如图
(1),在△ABC中,AB=AC,BD=AD,AC=CD,
∴∠B=∠C=∠BAD,∠CDA=∠CAD.
∵∠CDA=∠B+∠BAD=2∠B,
∴∠CAB=∠CAD+∠BAD=3∠B.
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°.
②如图
(2),在△ABC中,AB=AC,AD=BD=CD,
∴∠B=∠C=∠DAC=∠DAB,
∴∠BAC=2∠B,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°.

18.如图,将$\triangle ABC$沿着过 BC 的中点 D 的直线折叠,使点 B 落在边 AC 上的点$B_1$处,称为第一次操作,折痕 DE 到 AC 的距离为$h_1$,还原纸片后再将$\triangle BDE$沿着过 BD 的中点$D_1$的直线折叠,使点 B 落在边 DE 上的点$B_2$处,称为第二次操作,折痕$D_1E_1$到 AC 的距离记为$h_2$,按上述方法不断操作下去,经过第$n次操作后得到的折痕D_{n-1}E_{n-1}$到 AC 的距离记为$h_n$,若$h_1= 1$,则$h_n$的值为______2-$\frac{1}{2^{n-1}}$.

答案： 2-$\frac{1}{2^{n-1}}$ [解析]
∵将△ABC沿着过BC的中点D的直线折叠，使点B落在边AC上的点B₁处，
∴BD=CD=DB₁,∠BDE=∠B₁DE.
∴∠DCB₁=∠DB₁C.
∵∠CDB₁+∠BDE+∠B₁DE=180°,∠CDB₁+∠DCB₁+∠DB₁C=180°,
∴∠BDE=∠B₁DE=∠DCB₁=∠DB₁C.
∴DE//AC.
∵DE到AC的距离为h₁,
∴点B₁到DE的距离h₁=1.
由折叠的性质,得△EBD≌△EB₁D,
∴S△EBD=S△EB₁D,
∴点B到DE的距离=点B₁到DE的距离为h₁=1.
同理,D₁E₁//DE,点B到D₁E₁的距离=点B₂到D₁E₁的距离为$\frac{1}{2}$h₁=$\frac{1}{2}$.
∴B₁到D₁E₁的距离h₂=1+$\frac{1}{2}$.
同理h₃=h₂+$\frac{1}{4}$h₁=1+$\frac{1}{2}$+$\frac{1}{4}$,
h₄=h₃+$\frac{1}{8}$h₁=1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$,…,
hₙ=1+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{2^{n-1}}$=2-$\frac{1}{2^{n-1}}$.