第134页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
6. (2024·河北中考)已知a,b,n均为正整数.
(1)若n<√10<n+1,则n=
(2)若n-1<√a<n,n<√b<n+1,则满足条件的a的个数总比b的个数少
(1)若n<√10<n+1,则n=
3
;(2)若n-1<√a<n,n<√b<n+1,则满足条件的a的个数总比b的个数少
2
个.
答案:
(1)3
(2)2 [解析]
∵n−1<√a<n,
∴(n−1)²<a<n²,
∴a的个数为n²−(n−1)²−1=n²−n²+2n−1−1 =2n−2。
注意去括号时符号的变化
∵n<√b<n + 1,
∴n²<b<(n + 1)²,
∴b的个数为(n + 1)²−n²−1=n²+2n+1−n²−1=2n。
∵2n−(2n−2)=2,
∴满足条件的a的个数总比b的个数少2个。
(1)3
(2)2 [解析]
∵n−1<√a<n,
∴(n−1)²<a<n²,
∴a的个数为n²−(n−1)²−1=n²−n²+2n−1−1 =2n−2。
注意去括号时符号的变化
∵n<√b<n + 1,
∴n²<b<(n + 1)²,
∴b的个数为(n + 1)²−n²−1=n²+2n+1−n²−1=2n。
∵2n−(2n−2)=2,
∴满足条件的a的个数总比b的个数少2个。
7. (2024·镇江中考)等腰三角形的两边长分别为6和2,则第三边长为
6
.
答案:
6
8. (2024·深圳中考)如图,A,B,C均为正方形,若A的面积为10,C的面积为1,则B的边长可以是
2
.(写出一个答案即可)
答案:
2(答案不唯一)
9. (2024·湖南衡阳期末)勾股定理$a^2+b^2= c^2$本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫作勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),…,分析上面勾股数组可以发现4= 1×(3+1),12= 2×(5+1),24= 3×(7+1),…,依此规律,第5个勾股数组为
(11,60,61)
.
答案:
(11,60,61) [解析]由勾股数组(3,4,5),(5,12,13),(7,24,25),…,
得4=1×(3 + 1),12=2×(5 + 1),24=3×(7 + 1),
第4组勾股数中间的数为4×(9 + 1)=40,即勾股数为(9,40,41);
第5组勾股数中间的数为5×(11 + 1)=60,即(11,60,61)。
得4=1×(3 + 1),12=2×(5 + 1),24=3×(7 + 1),
第4组勾股数中间的数为4×(9 + 1)=40,即勾股数为(9,40,41);
第5组勾股数中间的数为5×(11 + 1)=60,即(11,60,61)。
10. (2024·潍坊中考)请写出同时满足以下两个条件的一个函数:
①y随着x的增大而减小;②函数图象与y轴正半轴相交.
y = −x + 2(答案不唯一)
.①y随着x的增大而减小;②函数图象与y轴正半轴相交.
答案:
y = −x + 2(答案不唯一)
11. (2024·江西赣州兴国期末)如图,在△ABC中,∠ACB= 90°,AC= 8 cm,BC= 14 cm,点P从点A出发沿A→C→B路径向终点运动,终点为点B,点Q从点B出发沿B→C→A路径向终点运动,终点为点A,点P和点Q分别以2 cm/s和3 cm/s的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过P和点Q作PE⊥l于点E,QF⊥l于点F.设运动时间为t秒,要使以点P,E,C为顶点的三角形与以点Q,F,C为顶点的三角形全等,则t的值为 .
答案:
22/5或6或8[解析]
∵PE⊥l于点E,QF⊥l于点F,
∴∠PEC=∠CFQ=90°,
∴∠QCF+∠CQF=90°。
∵∠ACB=90°,
∴∠PCE+∠QCF=90°,
∴∠PCE=∠CQF。
①当0≤t<4时,点P在AC上,点Q在BC上,如图
(1),此时有AP=2t cm,BQ=3t cm,AC=8 cm,BC=14 cm。当PC=QC,即8−2t=14−3t时,△PCE≌△CQF,解得t=6,不符合题意,舍去;
 ②当4≤t<14/3时,点P在BC上,点Q也在BC上,如图
②当4≤t<14/3时,点P在BC上,点Q也在BC上,如图
(2),若PC=QC,则点P与点Q重合,△CPE≌△CQF,即2t−8=14−3t,解得t=22/5;
③当14/3≤t<22/3时,点P在BC上,点Q在AC上,如图
(3),当PC=QC,即2t−8=3t−14时,△PCE≌△CQF,解得t=6;
 ④当22/3≤t≤11时,点Q停在点A处,点P在BC上,如图
④当22/3≤t≤11时,点Q停在点A处,点P在BC上,如图
(4),当PC=QC时,即2t−8=8时,△PCE≌△CQF,解得t=8。
综上所述,当t等于22/5或6或8时,以点P,E,C为顶点的三角形与以点Q,F,C为顶点的三角形全等。
22/5或6或8[解析]
∵PE⊥l于点E,QF⊥l于点F,
∴∠PEC=∠CFQ=90°,
∴∠QCF+∠CQF=90°。
∵∠ACB=90°,
∴∠PCE+∠QCF=90°,
∴∠PCE=∠CQF。
①当0≤t<4时,点P在AC上,点Q在BC上,如图
(1),此时有AP=2t cm,BQ=3t cm,AC=8 cm,BC=14 cm。当PC=QC,即8−2t=14−3t时,△PCE≌△CQF,解得t=6,不符合题意,舍去;
 ②当4≤t<14/3时,点P在BC上,点Q也在BC上,如图
②当4≤t<14/3时,点P在BC上,点Q也在BC上,如图(2),若PC=QC,则点P与点Q重合,△CPE≌△CQF,即2t−8=14−3t,解得t=22/5;
③当14/3≤t<22/3时,点P在BC上,点Q在AC上,如图
(3),当PC=QC,即2t−8=3t−14时,△PCE≌△CQF,解得t=6;
 ④当22/3≤t≤11时,点Q停在点A处,点P在BC上,如图
④当22/3≤t≤11时,点Q停在点A处,点P在BC上,如图(4),当PC=QC时,即2t−8=8时,△PCE≌△CQF,解得t=8。
综上所述,当t等于22/5或6或8时,以点P,E,C为顶点的三角形与以点Q,F,C为顶点的三角形全等。
12. (2024·淄博中考)如图,已知AB= CD,点E,F在线段BD上,且AF= CE.
请从①BF= DE;②∠BAF= ∠DCE;③AF= CF中选择一个合适的选项作为已知条件,使得△ABF≌△CDE.
你添加的条件是:
添加条件后,请证明AE//CF.
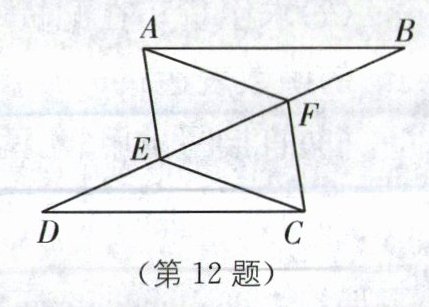
证明:在△ABF和△CDE中,{AB=CD,AF=CE,BF=DE},
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF。
在△ABE和△CDF中,{AB=CD,∠B=∠D,BE=DF},
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
请从①BF= DE;②∠BAF= ∠DCE;③AF= CF中选择一个合适的选项作为已知条件,使得△ABF≌△CDE.
你添加的条件是:
①
(只填写一个序号).添加条件后,请证明AE//CF.

证明:在△ABF和△CDE中,{AB=CD,AF=CE,BF=DE},
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF。
在△ABE和△CDF中,{AB=CD,∠B=∠D,BE=DF},
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
答案:
当选择①BF=DE时,△ABF≌△CDE。证明如下:
在△ABF和△CDE中,{AB=CD,AF=CE,BF=DE},
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF。
在△ABE和△CDF中,{AB=CD,∠B=∠D,BE=DF},
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
一题多解 当选择②∠BAF=∠DCE时,△ABF≌△CDE。证明如下:
在△ABF和△CDE中,{AB=CD,∠BAF=∠DCE,AF=CE},
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE,
同理可证△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
在△ABF和△CDE中,{AB=CD,AF=CE,BF=DE},
∴△ABF≌△CDE(SSS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF。
在△ABE和△CDF中,{AB=CD,∠B=∠D,BE=DF},
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
一题多解 当选择②∠BAF=∠DCE时,△ABF≌△CDE。证明如下:
在△ABF和△CDE中,{AB=CD,∠BAF=∠DCE,AF=CE},
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE,
同理可证△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF。
13. (2024·江西景德镇乐平期末)综合探究:
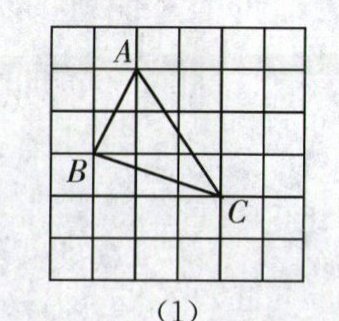
“在△ABC中,AB,BC,AC三边的长分别为√5,√10,√13,求这个三角形的面积.”
小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图(1)所示,这样不需要求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫作构图法.
(1)直接写出图(1)中△ABC的面积是 ;
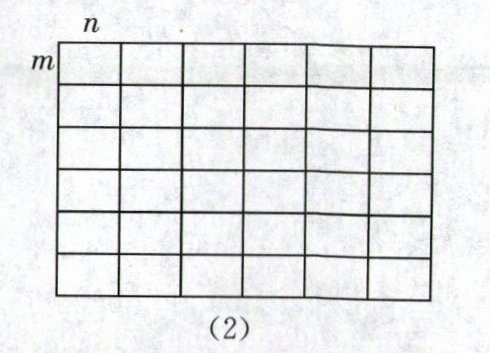
(2)若△MNP的边长分别为$√(m^2+16n^2),√(9m^2+4n^2),√(4m^2+4n^2)(m>0,n>0,$且m≠n),试运用构图法在图(2)中画出相应的△MNP,并求出△MNP的面积;
(3)拓展应用:求代数式$√(x^2+1)+√((4-x)^2+4)(0≤x≤4)$的最小值.
“在△ABC中,AB,BC,AC三边的长分别为√5,√10,√13,求这个三角形的面积.”
小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图(1)所示,这样不需要求△ABC的高,而借用网格就能计算出它的面积.我们把上述求△ABC面积的方法叫作构图法.
(1)直接写出图(1)中△ABC的面积是 ;
(2)若△MNP的边长分别为$√(m^2+16n^2),√(9m^2+4n^2),√(4m^2+4n^2)(m>0,n>0,$且m≠n),试运用构图法在图(2)中画出相应的△MNP,并求出△MNP的面积;
(3)拓展应用:求代数式$√(x^2+1)+√((4-x)^2+4)(0≤x≤4)$的最小值.


答案:
(1)3.5
(2)如图
(1),由勾股定理,知MN=√(m²+16n²),NP=√(9m²+4n²),PM=√(4m²+4n²),△MNP即为所求作。

△MNP的面积为3m×4n−1/2×m×4n−1/2×2m×2n−1/2×3m×2n=12mn−2mn−2mn−3mn=5mn。
(3)√(x²+1)可看作两直角边分别为x和1的Rt△ACP的斜边长,√((4−x)²+4)可看作两直角边分别是4−x和2的Rt△BDP的斜边长,构造图形如图
(2),

依题意,得AC=1,DB = 2,CD = 4,CP=x,PD=4−x,求代数式√(x²+1)+√((4−x)²+4)(0≤x≤4)的最小值,就是求AP+BP的最小值,当A,P,B共线时,AP+BP为最小,最小值为AB的长。
∵AE=AC+CE=1+2=3,BE=CD=4,
∴AB=√(AE²+BE²)=√(3²+4²)=5,
∴代数式√(x²+1)+√((4−x)²+4)(0≤x≤4)的最小值是5。
(1)3.5
(2)如图
(1),由勾股定理,知MN=√(m²+16n²),NP=√(9m²+4n²),PM=√(4m²+4n²),△MNP即为所求作。

△MNP的面积为3m×4n−1/2×m×4n−1/2×2m×2n−1/2×3m×2n=12mn−2mn−2mn−3mn=5mn。
(3)√(x²+1)可看作两直角边分别为x和1的Rt△ACP的斜边长,√((4−x)²+4)可看作两直角边分别是4−x和2的Rt△BDP的斜边长,构造图形如图
(2),

依题意,得AC=1,DB = 2,CD = 4,CP=x,PD=4−x,求代数式√(x²+1)+√((4−x)²+4)(0≤x≤4)的最小值,就是求AP+BP的最小值,当A,P,B共线时,AP+BP为最小,最小值为AB的长。
∵AE=AC+CE=1+2=3,BE=CD=4,
∴AB=√(AE²+BE²)=√(3²+4²)=5,
∴代数式√(x²+1)+√((4−x)²+4)(0≤x≤4)的最小值是5。
查看更多完整答案,请扫码查看


