《2025年实验班提优大考卷八年级数学上册苏科版》

1.(2024·南京秦淮区钟英中学模拟)绝对值小于$\sqrt{5}$的整数的个数是(D).
A.2
B.3
C.4
D.5

答案： D

2.(2024·巴中中考)在0,1,-1,π中最小的实数是(B).
A.0
B.-1
C.1
D.π

答案： B

3.(2024·盐城阜宁期末)满足下列条件的△ABC不是直角三角形的是(D).
A.$BC= 1,AC= 2,AB= \sqrt{3}$
B.$BC:AC:AB= 3:4:5$
C.$\angle A+\angle B= \angle C$
D.$\angle A:\angle B:\angle C= 3:4:5$

答案： D

4.如图,点C是线段AB上的一点,分别以AC,BC为边向两侧作正方形.设$AB= 6$,两个正方形的面积和$S_{1}+S_{2}= 20$,则图中△BCD的面积为(A).

A.4
B.6
C.8
D.10

答案： A

5.(2024·盐城中考)矩形相邻两边长分别为$\sqrt{2}\ cm,\sqrt{5}\ cm$,设其面积为$S\ cm^{2}$,则S在哪两个连续整数之间(C).
A.1和2
B.2和3
C.3和4
D.4和5

答案： C

6.(2025·苏州外国语学校月考)下列说法:①$\sqrt{(-10)^{2}}= -10$;②数轴上的点与实数成一一对应关系;③任何实数不是有理数就是无理数;④两个无理数的和还是无理数;⑤-2是4的平方根.正确的个数为(C).
A.1
B.2
C.3
D.4

答案： C

7.若$\sqrt{a+b+5}+|2a-b+1|= 0$,则$(b-a)^{2025}=$(-1).
A.-1
B.1
C.$5^{2023}$
D.$-5^{2023}$

答案： A [解析]
∵√(a+b+5)≥0,|2a-b+1|≥0,
∴当√(a+b+5)+|2a-b+1|=0时，√(a+b+5)=0,|2a-b+1|=0.
∴a+b+5=0,2a-b+1=0,
∴a=-2,b=-3,
∴$(b-a)^2025=(-3+2)^2025=-1.$故选A.

8.(2024·福建福州屏东中学期末)汉代数学家赵爽为了证明勾股定理,创制了一幅"赵爽弦图".如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为$S_{1},S_{2},S_{3}$.若$S_{1}+S_{2}+S_{3}= 2025$,则$S_{2}$的值是(D).

A.567
B.666
C.777
D.675

答案： D [解析]
∵八个直角三角形全等,四边形ABCD,EFGH,MNKT 是正方形,
∴CG=NG,CF=DG=NF,
∴$S₁=(CG+DG)^2=CG^2+DG^2+2CG·DG=GF^2+2CG·DG,S₂=GF^2,S₃=(NG-NF)^2=NG^2+NF^2-2NG·NF,$
∴$S₁+S₂+S₃=GF^2+2CG·DG+GF^2+NG^2+NF^2-2NG·NF=3GF^2=2025,$
∴$GF^2=675,$
∴S₂=675.故选D.

9.(2024·常州模拟)在比$\sqrt{5}-1$小的数中,最大的整数是1.

答案： 1

10.(2024·包头中考)计算:$\sqrt[3]{8}+(-1)^{2024}=$3.

答案： 3

11.(2024·西宁中考)如图,正方形ABCD的边长为4,以AB边为底向外作等腰直角三角形ABE,点P是对角线AC上的一个动点,连接PB,PE,则$PB+PE$的最小值是______.

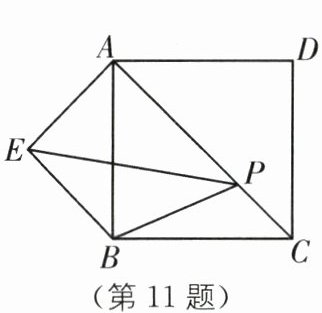
答案：
√40 [解析]如图,作点 B 关于直线 AC 的对称点,正好落于点 D,连接 ED 交 AC 于点 P,连接 PE,PB,此时 PB+PE 的值最小.

由作图可知,PB=PD,DE=PB+PE,
∵正方形 ABCD 的边长为 4,△ABE 是等腰直角三角形,
∴$EB=EA=√8,BD=√(4^2+4^2)=√32,∠EBD=45°+45°=90°,$
∴在 Rt△EBD 中$,ED=√(EB^2+BD^2)=√(8+32)=√40,$
∴PB+PE 的最小值√40.