第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
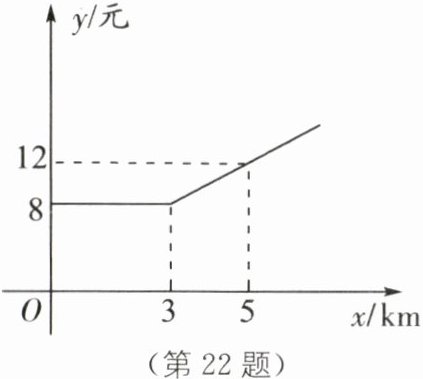
22.(10分)某市出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下列问题:
(1)出租车的起步价是多少元?
(2)当$x>3$时,求y关于x的函数关系式.
(3)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
(1)出租车的起步价是多少元?
(2)当$x>3$时,求y关于x的函数关系式.
(3)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.

答案:
(1)由题图可知出租车的起步价是8元.
(2)当x > 3时,设y与x的函数关系式为y = kx + b(k ≠ 0).
由函数图象,得{8 = 3k + b,12 = 5k + b},解得{k = 2,b = 2}.
故y与x的函数关系式为y = 2x + 2(x > 3).
(3)
∵32元 > 8元,
∴当y = 32时,32 = 2x + 2,解得x = 15.故这位乘客乘车的里程是15 km.
(1)由题图可知出租车的起步价是8元.
(2)当x > 3时,设y与x的函数关系式为y = kx + b(k ≠ 0).
由函数图象,得{8 = 3k + b,12 = 5k + b},解得{k = 2,b = 2}.
故y与x的函数关系式为y = 2x + 2(x > 3).
(3)
∵32元 > 8元,
∴当y = 32时,32 = 2x + 2,解得x = 15.故这位乘客乘车的里程是15 km.
23.(10分)新情境 进货方案选择 (2024·广元中考)近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购迸长、短两款传统服饰进行销售,进货价和销售价如表:
| | 短款 | 长款 |
| 进货价/(元/件) | 80 | 90 |
| 销售价/(元/件) | 100 | 120 |

(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数.
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
| | 短款 | 长款 |
| 进货价/(元/件) | 80 | 90 |
| 销售价/(元/件) | 100 | 120 |

(1)该服装店第一次用4300元购进长、短两款服装共50件,求两款服装分别购进的件数.
(2)第一次购进的两款服装售完后,该服装店计划再次购进长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
答案:
(1)设购进短款服装x件,购进长款服装y件,
由题意,得{x + y = 50,80x + 90y = 4300},
∴{x = 20,y = 30}.
故短款服装购进20件,长款服装购进30件.
(2)设第二次购进m件短款服装,则购进(200 - m)件长款服装,
得80m + 90(200 - m) ≤ 16800,
∴m ≥ 120.
设利润为w元,
则w = (100 - 80)m + (120 - 90)(200 - m)= -10m + 6000.
∵ -10 < 0,
∴w随m的增大而减小,
∴当m = 120时,利润w最大为 -10×120 + 6000 = 4800(元).
故当购进120件短款服装,80件长款服装时有最大利润,最大利润是4800元.
(1)设购进短款服装x件,购进长款服装y件,
由题意,得{x + y = 50,80x + 90y = 4300},
∴{x = 20,y = 30}.
故短款服装购进20件,长款服装购进30件.
(2)设第二次购进m件短款服装,则购进(200 - m)件长款服装,
得80m + 90(200 - m) ≤ 16800,
∴m ≥ 120.
设利润为w元,
则w = (100 - 80)m + (120 - 90)(200 - m)= -10m + 6000.
∵ -10 < 0,
∴w随m的增大而减小,
∴当m = 120时,利润w最大为 -10×120 + 6000 = 4800(元).
故当购进120件短款服装,80件长款服装时有最大利润,最大利润是4800元.
查看更多完整答案,请扫码查看


