《2025年实验班提优大考卷八年级数学上册苏科版》

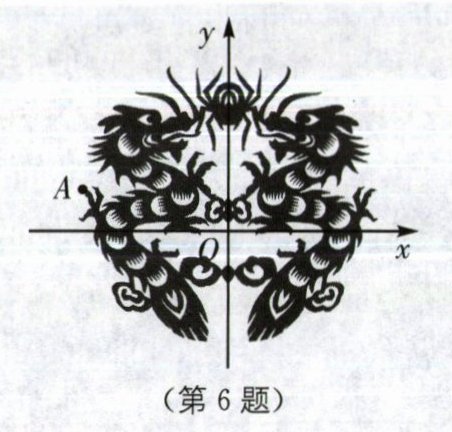
6. (2024·通辽中考)剪纸是我国民间艺术之一,如图放置的剪纸作品,它的对称轴与平面直角坐标系的坐标轴重合,则点A(-4,2)关于对称轴对称的点的坐标为(C).

A.(-4,-2)
B.(4,-2)
C.(4,2)
D.(-2,-4)

答案： C

7. (2024·甘肃中考)如图(1),“燕几”即宴几,是世界上最早的一套组合桌,由北宋进士黄伯思设计.全套“燕几”一共有七张桌子,包括两张长桌、两张中桌和三张小桌,每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图(2)给出了《燕几图》中名称为“回文”的桌面拼合方式,若设每张桌面的宽为x尺,长桌的长为y尺,则y与x的关系可以表示为(B).
A.$y= 3x$
B.$y= 4x$
C.$y= 3x+1$
D.$y= 4x+1$

答案： B

8. (2025·长沙宁乡一模)勾股定理最早出现在商高的《周髀算经》：“勾广三,股修四,经隅五”,我国古代把直角三角形的直角边中较小者称为“勾”,另一长直角边称为“股”,把斜边称为“弦”.观察下列勾股数：3,4,5；5,12,13；7,24,25；…,这类勾股数的特点是勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如：6,8,10；8,15,17；…,若此类勾股数的勾为10,则其弦是______26.

答案： 26　[解析]根据题意，得若a,b,c是符合同样规律的一组勾股数，a=m(m为偶数且m≥4)，则另一条直角边$b=(\frac{m}{2})^{2}-1$，弦$c=(\frac{m}{2})^{2}+1$.故弦为$(\frac{10}{2})^{2}+1=26$.

9. (2024·吉林中考)图(1)中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图(2),其中AB= AB',AB⊥B'C于点C,BC= 0.5尺,B'C= 2尺.设AC的长度为x尺,可列方程为$x^{2}+2^{2}=(x+0.5)^{2}$.

答案： $x^{2}+2^{2}=(x+0.5)^{2}$

10. (2025·茂名电白区模拟)元朝朱世杰的《算学启蒙》一书记载：“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之.”意思是：现有良马每天行走240里,驽马每天行走150里,驽马先走12天,问良马几天可以追上驽马？两匹马行走路程s(里)与行走时间t(日)的函数关系如图所示,则图中交点P的坐标是______.
(32,4800)

答案： (32,4800)　[解析]设良马t天可以追上驽马.
　　根据题意，得$240t=150(t+12)$，解得$t=20$.
∴良马20天可以追上驽马，此时良马所行路程为$240×20=4800$(里)，
∴点P的坐标为(32,4800).
解后反思本题考查一次函数与一元一次方程的应用，解题的关键是列方程求出良马追上驽马的天数，从而求出良马所行路程.

11. (2024·安徽中考)我国古代数学家张衡将圆周率取值为$\sqrt{10}$,祖冲之给出圆周率的一种分数形式的近似值为$\frac{22}{7}$,比较大小：$\sqrt{10}$＞$\frac{22}{7}$(填“＞”或“＜”).

答案： ＞

12. 中国是发现和研究勾股定理最古老的国家之一,中国古代称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,其中勾长、股长的平方和等于弦长的平方,即为“勾股定理”,勾股定理是几何学中一颗光彩夺目的明珠,在几何问题中有着广泛的应用.如图,在直线l上依次摆放着五个正方形.已知斜放置的两个正方形的面积分别是2,3,正放置的三个正方形的面积依次是$S_1,S_2,S_3$,则$S_1+2S_2+S_3$等于______.

答案：
5　[解析]如图.
　　　
∵图中的四边形均为正方形，
∴$\angle ABD=90^{\circ}$，$AB=DB$，$\angle ACB=90^{\circ}$，
∴$\angle ABC+\angle DBE=90^{\circ}$，$\angle ABC+\angle CAB=90^{\circ}$，
∴$\angle CAB=\angle DBE$.
　在$\triangle ABC$和$\triangle BDE$中，$\begin{cases} \angle ACB=\angle BED \\ \angle CAB=\angle EBD \\ AB=BD \end{cases}$
∴$\triangle ABC\cong \triangle BDE(AAS)$，
∴$AC=BE$.
∵$DE^{2}+BE^{2}=DB^{2}$，
∴$DE^{2}+AC^{2}=DB^{2}$.
∵$S_{1}=AC^{2}$，$S_{2}=DE^{2}$，$DB^{2}=2$，
∴$S_{1}+S_{2}=2$，同理可得$S_{2}+S_{3}=3$，
∴$S_{1}+2S_{2}+S_{3}=2+3=5$.
思路引导结合正方形的性质证明$\triangle ABC\cong \triangle BDE$，根据全等三角形的性质推出$S_{1}+S_{2}=2$，同理可得$S_{2}+S_{3}=3$，据此求解即可.本题考查了全等三角形的判定与性质，结合正方形的性质证明$\triangle ABC\cong \triangle BDE$是解题的关键.