第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
1.(2025·泰州靖江市期末)下列各组数中,是勾股数的是(
A.1,2,3
B.5,12,13
C.0.3,0.4,0.5
D.4,6,8
B
).A.1,2,3
B.5,12,13
C.0.3,0.4,0.5
D.4,6,8
答案:
B
2.(2025·徐州沛县期末)下列条件中,不能判断△ABC 为直角三角形的是(
A.a= 1.5,b= 2,c= 2.5
B.a:b:c= 3:4:5
C.∠A+∠B= ∠C
D.∠A:∠B:∠C= 3:4:5
D
).A.a= 1.5,b= 2,c= 2.5
B.a:b:c= 3:4:5
C.∠A+∠B= ∠C
D.∠A:∠B:∠C= 3:4:5
答案:
D
3.若等腰三角形的底边长为 6,底边上的中线长为 4,它的腰长为(
A.6
B.7
C.8
D.5
D
).A.6
B.7
C.8
D.5
答案:
D
4.(苏州自主招生)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若 a= 3,b= 4,则该长方形的面积为(

A.20
B.24
C.$\frac{99}{4}$
D.$\frac{53}{2}$
B
).
A.20
B.24
C.$\frac{99}{4}$
D.$\frac{53}{2}$
答案:
B [解析]设小正方形的边长为 x,
∵a=3,b=4,
∴AB=3+4=7。在 Rt△ABC 中,AC²+BC²=AB²,即(3+x)²+(x+4)²=7²,整理,得 x²+7x=12,而长方形面积为(x+3)(x+4)=x²+7x+12=12+12=24,无需求 x 的值,只需代入 x²+7x=12 即可。
∴该长方形的面积为 24。故选 B。思路引导:欲求长方形的面积,则求出小正方形的边长即可,由此可设小正方形的边长为 x,在直角三角形 ABC 中,利用勾股定理可建立关于 x 的方程,利用整体代入的思想解决问题,进而可求出该长方形的面积。
∵a=3,b=4,
∴AB=3+4=7。在 Rt△ABC 中,AC²+BC²=AB²,即(3+x)²+(x+4)²=7²,整理,得 x²+7x=12,而长方形面积为(x+3)(x+4)=x²+7x+12=12+12=24,无需求 x 的值,只需代入 x²+7x=12 即可。
∴该长方形的面积为 24。故选 B。思路引导:欲求长方形的面积,则求出小正方形的边长即可,由此可设小正方形的边长为 x,在直角三角形 ABC 中,利用勾股定理可建立关于 x 的方程,利用整体代入的思想解决问题,进而可求出该长方形的面积。
5.(2025·镇江金坛区期中)如图,在 Rt△ABC 中,∠C= 90°,AC= 8,BC= 6,D 为 AC 上一点.若 BD 是∠ABC 的平分线,则 AD 的长是( ).

A.3
B.4
C.5
D.6

A.3
B.4
C.5
D.6
答案:
C [解析]如图,过点 D 作 AB 的垂线,垂足为 P。

在 Rt△ABC 中,AC=8,BC=6,由勾股定理,得 AB=$\sqrt{AC^2+BC^2}=\sqrt{8^2+6^2}=10$。
∵BD 是∠ABC 的平分线,
∴∠CBD=∠PBD。在△BDC 和△BDP 中,$\left\{\begin{array}{l} ∠CBD=∠PBD,\\ ∠C=∠BPD=90^{\circ },\\ BD=BD,\end{array}\right. $
∴△BDC≌△BDP(AAS),
∴BC=BP=6,CD=PD。设 CD=PD=x,在 Rt△ADP 中,PA=AB - BP=4,AD=8 - x,由勾股定理,得 x²+4²=(8 - x)²,解得 x=3,
∴AD=5。故选 C。
C [解析]如图,过点 D 作 AB 的垂线,垂足为 P。

在 Rt△ABC 中,AC=8,BC=6,由勾股定理,得 AB=$\sqrt{AC^2+BC^2}=\sqrt{8^2+6^2}=10$。
∵BD 是∠ABC 的平分线,
∴∠CBD=∠PBD。在△BDC 和△BDP 中,$\left\{\begin{array}{l} ∠CBD=∠PBD,\\ ∠C=∠BPD=90^{\circ },\\ BD=BD,\end{array}\right. $
∴△BDC≌△BDP(AAS),
∴BC=BP=6,CD=PD。设 CD=PD=x,在 Rt△ADP 中,PA=AB - BP=4,AD=8 - x,由勾股定理,得 x²+4²=(8 - x)²,解得 x=3,
∴AD=5。故选 C。
6.如图,在△ABC 中,∠C= 90°,点 D 为 AC 上一点,点 E 是 AB 上一点,且∠BDE= 90°,DB= DE= AE,若 BC= 5,则 AD 的长是( ).

A.7
B.9.5
C.5
D.10

A.7
B.9.5
C.5
D.10
答案:
D [解析]过点 E 作 EF⊥AC 于点 F,如图。

∵∠BDE=90°,
∴∠EDF=90° - ∠BDC=∠DBC。在△BDC 和△DEF 中,$\left\{\begin{array}{l} ∠C=∠EFD,\\ ∠DBC=∠EDF,\\ BD=DE,\end{array}\right. $
∴△BDC≌△DEF(AAS),
∴DF=BC=5。
∵DE=AE,EF⊥AC,
∴AD=2DF=10。故选 D。
D [解析]过点 E 作 EF⊥AC 于点 F,如图。

∵∠BDE=90°,
∴∠EDF=90° - ∠BDC=∠DBC。在△BDC 和△DEF 中,$\left\{\begin{array}{l} ∠C=∠EFD,\\ ∠DBC=∠EDF,\\ BD=DE,\end{array}\right. $
∴△BDC≌△DEF(AAS),
∴DF=BC=5。
∵DE=AE,EF⊥AC,
∴AD=2DF=10。故选 D。
7.传统文化 《九章算术》 (2024·宿迁宿城区期中)我国古代数学著作《九章算术》中记载了一个问题:"今有池方一丈,葭(jiā)生其中,出水一尺.引葭赴岸,适与岸齐.问水深几何."(丈、尺是长度单位,1 丈= 10 尺)其大意为有一个水池,水面是一个边长为 10 尺的正方形,在水池正中央有一根芦苇,它高出水面 1 尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,如图,那么水深为(
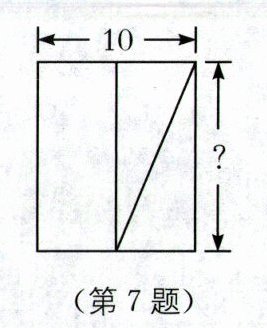
A.10 尺
B.11 尺
C.12 尺
D.13 尺
C
).
A.10 尺
B.11 尺
C.12 尺
D.13 尺
答案:
C [解析]设水深为 h 尺,则芦苇长为(h + 1)尺,根据勾股定理,得(h + 1)² - h²=(10÷2)²,解得 h=12,
∴水深为 12 尺。故选 C。
∴水深为 12 尺。故选 C。
8.(2025·无锡宜兴实验教育集团月考)如图,在△ABC 中,AB= 6,AC= 9,AD⊥BC 于 D,M 为 AD 上任一点,则 $MC^2-MB^2$ 等于(
A.29
B.32
C.36
D.45
D
).A.29
B.32
C.36
D.45
答案:
D [解析]在 Rt△ABD 和 Rt△ADC 中,BD²=AB² - AD²,CD²=AC² - AD²。在 Rt△BDM 和 Rt△CDM 中,BM²=BD²+MD²=AB² - AD²+MD²,MC²=CD²+MD²=AC² - AD²+MD²,
∴MC² - MB²=(AC² - AD²+MD²)-(AB² - AD²+MD²)=AC² - AB²=45。故选 D。
∴MC² - MB²=(AC² - AD²+MD²)-(AB² - AD²+MD²)=AC² - AB²=45。故选 D。
查看更多完整答案,请扫码查看


