《2025年实验班提优大考卷八年级数学上册苏科版》

11.(2025·湖南模拟)在平面直角坐标系中,直线l经过第一、三、四象限.若点$A(a,1),B(0,b)$都在直线l上,则a______b.(填“＞”“＜”或“=”)

答案：
＞　[解析]直线l经过第一、三、四象限，如图
　　　　　　　　
由图可知，a ＞ 0，b ＜ 0，
∴a ＞ b.
思路引导：本题考查一次函数的性质，解题的关键是画出一次函数大致图象解决问题.

12.(2024·上海中考)某种商品的销售量y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额1000万元,当投入90万元时销售量5000万元,则投入80万元时,销售额为4500万元.

答案： 4500

13.已知一次函数$y= -2x+1$,若$-2≤x≤1$,则y的最小值为-1.

答案： -1

14.(2024·辽宁大连高新区期末)如图,在平面直角坐标系xOy中,点$A(0,2),B(1,0)$,以点B为中心,把线段BA顺时针旋转$90^{\circ}$得到线段BC,则点C的坐标为(3,1).

答案： (3,1)

15.(2025·山东菏泽期末)已知平面直角坐标系中点$A(-2,1)$,过点A作直线$AB⊥x$轴,如果$AB= 3$,且点B位于第三象限,则点B的坐标为(-2,-2).

答案： (-2,-2)

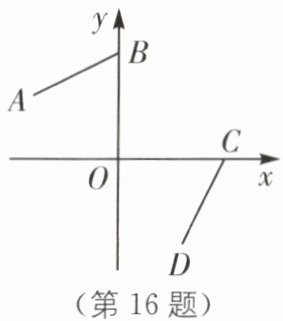
16.(2024·常州金坛区期中)如图,在平面直角坐标系中,点A的坐标是(-4,3),点B的坐标是(0,5),将线段AB绕原点按顺时针方向旋转得到线段CD(点C,D分别与点A,B对应).若点C恰好落在x轴上,则点D的坐标是______.

答案：
(3,-4)　[解析]如图，连接OA，OD，过点A和点D分别作y轴和x轴的垂线，垂足分别为M和N.
　　　　　　　　
∵点A坐标为(-4,3)，
∴AM = 4，MO = 3，
∴AO = √(3² + 4²)= 5.
∵B点坐标为(0,5)，
∴OB = 5.
由旋转，得OD = OB = 5，OC = OA = 5，∠AOC = ∠BOD，
∴AO = OD，∠AOC - ∠BOC = ∠BOD - ∠BOC，
∴∠AOB = ∠COD.
在△AMO和△DNO中，{∠AMO = ∠DNO，∠AOB = ∠COD，AO = OD}，
∴△AMO ≌ △DNO(AAS)，
∴ON = OM = 3，DN = AM = 4，
∴点D的坐标为(3,-4).

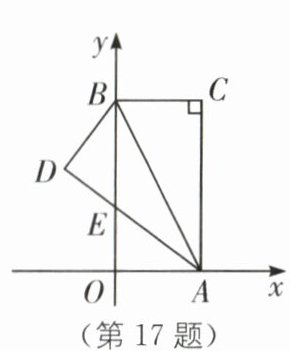
17.(2024·扬州广陵区期末)如图,在直角坐标系中,$Rt\triangle ABC$的顶点A在x轴上,顶点B在y轴上,$\angle ACB= 90^{\circ},OB//AC$,点C的坐标为(4,8),点D和点C关于AB成轴对称,且AD交y轴于点E,则点E的坐标为______(0,3).

答案： (0,3)　[解析]因为∠ACB = 90°，OB//AC，
所以∠OBC = 90°.
因为点C的坐标为(4,8)，所以AC = 8，BC = 4，
所以BD = BC = 4，AD = AC = 8.
因为点D和点C关于AB成轴对称，
所以∠CAB = ∠DAB.
又OB//AC，所以∠OBA = ∠CAB，
所以∠OBA = ∠DAB，所以BE = AE.
令BE = AE = x，则DE = 8 - x.
在Rt△BDE中，BD² + DE² = BE²，
即4² + (8 - x)² = x²，解得x = 5，
所以BE = 5，所以OE = 8 - 5 = 3，
即点E的坐标为(0,3).

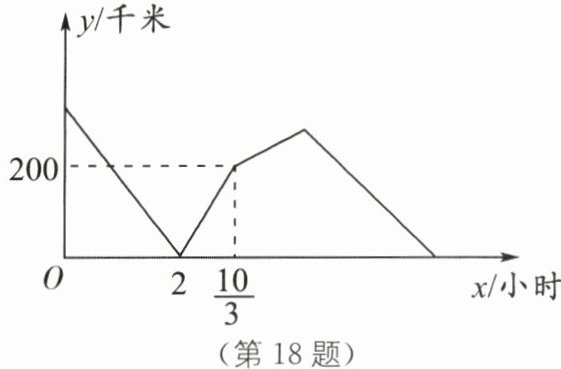
18.甲、乙两车分别从A,B两地同时出发,以各自的速度匀速相向而行.当甲车到达B地后,发现有重要物品需要送给乙车,于是甲车司机立即通知乙车(通知时间忽略不计),乙车接到通知后将速度降低50%继续匀速行驶,甲车司机花一定的时间准备好相关物品后,以原速的$\frac{4}{3}$倍匀速前去追赶乙车,当甲车追上乙车时,乙车恰好到达A地.如图反映的是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系,则甲车在B地准备好相关物品共花了______小时.

$\frac{5}{6}$

答案： 5/6　[解析]点(10/3,200)说明甲用10/3小时从A地行驶到B地，此时乙行驶了200千米，则乙的速度为v乙 = 200÷(10/3)= 60(千米/时).
两车2小时相遇，相遇后甲、乙都行驶了10/3 - 2 = 4/3(小时)，共行驶了200千米，则甲、乙的速度和为200÷(4/3)= 150(千米/时).又乙的速度为60千米/时，则甲的速度为90千米/时.
甲、乙2小时相遇，则A、B两地的距离为2×(60 + 90)= 300(千米).
设甲准备了x个小时，则甲、乙的距离为(200 + 30x)千米，则甲行驶300千米用的时间和乙行驶[300 - (200 + 30x)]千米用的时间相同，此时甲的速度为90×(4/3)= 120(千米/时)，乙的速度为60×50% = 30(千米/时)，即300/120 = [300 - (200 + 30x)]/30，解得x = 5/6.
故甲车在B地准备好相关物品共花了5/6小时.

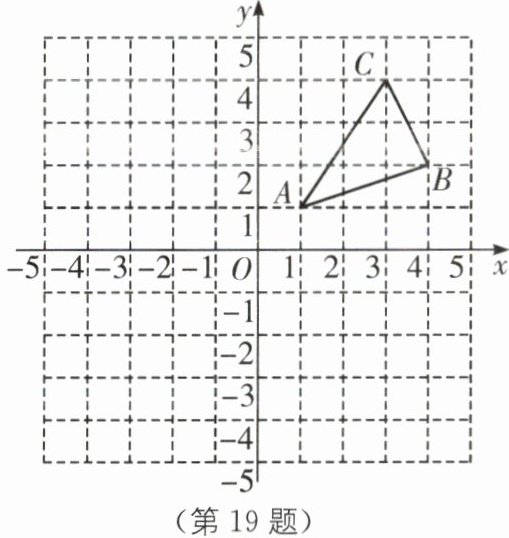
19.(8分)(2024·南通海安期中)如图,$\triangle ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)$.
(1)请写出$\triangle ABC$关于x轴对称的$\triangle A_1B_1C_1$的各顶点坐标；
(2)请画出$\triangle ABC$关于y轴对称的$\triangle A_2B_2C_2$；
(3)在x轴上求作一点P,使点P到A,B两点的距离和最小,请标出点P,并直接写出点P的坐标______.

答案：

(1)
∵△ABC与△A₁B₁C₁关于x轴对称，
∴点A₁(1,-1)，B₁(4,-2)，C₁(3,-4).
(2)如图，△A₂B₂C₂即为所求.
　　　　　
(3)如图，点P即为所求，点P的坐标为(2,0).