《2025年实验班提优大考卷八年级数学上册苏科版》

1.(2025·盐城盐都区期中)△ABC的三条边的长分别为a,b,c,下列条件不能判断△ABC是直角三角形的是(A).
A.∠A:∠B:∠C= 3:4:5
B.∠A= ∠B+∠C

$C.b^2= a^2-c^2$
D.a= 5,b= 12,c= 13

答案： A

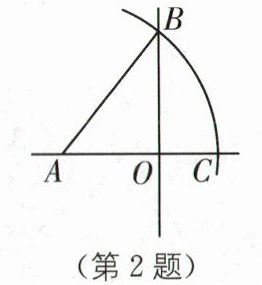
2.(2025·常州武进区期中)如图,直线AO,OB相交于点O,且AO⊥OB,线段AO= 3,OB= 4,以点A为圆心,以AB长为半径作弧,交射线AO于点C,则OC的长为(D).

A.5
B.4
C.3
D.2

答案： D [解析]直线 AO,OB 相交于点 O,且 AO⊥OB，
∴∠AOB=90°.在直角三角形 AOB 中,AO=3,OB=4.由勾股定理,得 AB=√(AO²+OB²)=√(3²+4²)=5,
∴AC=AB=5,
∴OC=AC - OA=5 - 3=2.故选 D.

3.(2024·镇江句容期中)将一根长24 cm的筷子置于底面直径为12 cm,高为5 cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是(B).
A.h≤19
B.11≤h≤19
C.12≤h≤19
D.13≤h≤19

答案： B [解析]如图,当筷子的底端在点 D 时,筷子露在杯子外面的长度最长,此时 h=24 - 5=19(cm);当筷子的底端在点 A 时,筷子露在杯子外面的长度最短.连接 AD,在 Rt△ABD 中,AD=12cm,BD=5cm,
∴AB²=AD²+BD²=169,
∴AB=13(cm),此时 h=24 - 13=11(cm),所以 h 的取值范围是 11≤h≤19.故选 B.

4. 传统文化 《九章算术》《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者几何?题意是:一根竹子原高1丈(1丈= 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?设折断处离地面的高度为x尺,则可列方程为(D).
$A.x^2-3= (10-x)^2$
$B.x^2-3^2= (10-x)^2$
$C.x^2+3= (10-x)^2$
$D.x^2+3^2= (10-x)^2$

答案： D [解析]
∵竹子原高 1 丈(1 丈=10 尺),且折断处离地面的高度为 x 尺,
∴折断处到竹梢触地面处的长度为(10 - x)尺,根据题意,得 x²+3²=(10 - x)².故选 D.

5.《九章算术》中有一题:今有开门去阃十寸,不合二寸,问门广几何?大意是:如图,从点O(O是AB的中点)处推开双门,点C与点D距离门槛AB的距离CE,DF都为10寸,双门间隙C,D的距离为2寸(即EF为2寸).根据题意可列出的等量关系是(C).
$A.AC^2+10^2= (AC-2÷2)^2$
$B.AC^2+(AC-2÷2)^2= 10^2$
$C.AC^2-(AC-2÷2)^2= 10^2$
$D.AC^2+10^2= (AC+2)^2$

答案： C [解析]由题意,得 AC=AO=BD=BO,OE=OF.
∵EF=2 寸,CE=DF=10 寸,
∴OE=OF=2÷2=1(寸),
∴AE=AO - OE=AC - OE=AC - 1.在 Rt△ACE 中,由勾股定理,得 AC² - AE²=CE²,即 AC² - (AC - 1)²=10².故选 C.

6. 新情境 举办新年晚会 为了迎接新年的到来,同学们做了许多拉花布置教室,准备举办新年晚会,大林搬来一架高为2.5米的木梯,准备把拉花挂到高为2.4米的墙上,开始梯脚与墙角的距离为1.5米,但高度不够.要想正好挂好拉花,梯脚应向前移动(人的高度忽略不计)(B).
A.0.7米
B.0.8米
C.0.9米
D.1.0米

答案： B [解析]由题意,得 2.5² - 2.4²=0.49,
∴移动后梯脚与墙角的距离为 0.7 米.
∵开始梯脚与墙角的距离为 1.5 米,
∴要想正好挂好拉花,梯脚应向前移动 1.5 - 0.7=0.8(米).故选 B.

7.木工师傅要做一扇长方形纱窗,做好后量得长为6分米,宽为4分米,对角线为7分米,则这扇纱窗不合格.(填“合格”或“不合格”)

答案： 不合格

8. 实验班原创 如图,一棵树在离地面3米处折断倒下,倒下后树尖到树根的距离为4米,这棵树在折断前的高度为8米.

答案： 8