第131页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
5.(2024·甘孜州中考)如图,在一个平面区域内,一台雷达探测器测得在点A,B,C处有目标出现.按某种规则,点A,B的位置可以分别表示为(1,90°),(2,240°),则点C的位置可以表示为
(3,30°)
.
答案:
(3,30°)
6.(2024·湖北中考)铁的密度为$7.9 g/cm^3,$铁块的质量m(单位:g)与它的体积V(单位$:cm^3)$之间的函数关系式为m= 7.9V,当$V= 10 cm^3$时,m=
79
g.
答案:
79
7.(2024·陕西中考)实验表明,在某地,温度在15 ℃至25 ℃的范围内,一种蟋蟀1 min的平均鸣叫次数y可近似看成该地当时温度x(℃)的一次函数.已知这种蟋蟀在温度为16 ℃时,1 min平均鸣叫92次;在温度为23 ℃时,1 min平均鸣叫155次.
(1)求y与x之间的函数表达式.
(2)当这种蟋蟀1 min平均鸣叫128次时,该地当时的温度约是多少?
(1)求y与x之间的函数表达式.
(2)当这种蟋蟀1 min平均鸣叫128次时,该地当时的温度约是多少?
答案:
7.
(1)设y与x之间的函数表达式为y=kx+b(k,b为常数,且k≠0).将x=16,y=92和x=23,y=155分别代入y=kx+b,得{16k+b=92,23k+b=155,解得{k=9,b=-52,
∴y与x之间的函数表达式为y=9x-52.
(2)将y=128代入y=9x-52,
得9x-52=128,解得x=20,
∴该地当时的温度约是20℃.
(1)设y与x之间的函数表达式为y=kx+b(k,b为常数,且k≠0).将x=16,y=92和x=23,y=155分别代入y=kx+b,得{16k+b=92,23k+b=155,解得{k=9,b=-52,
∴y与x之间的函数表达式为y=9x-52.
(2)将y=128代入y=9x-52,
得9x-52=128,解得x=20,
∴该地当时的温度约是20℃.
8.小明同学通过查阅资料发现,声音在空气中传播的速度随气温的变化而变化,几组对应值如下表:
|气温/℃|0|5|10|15|20|25|
|声音在空气中的传播速度/(m/s)|331|334|337|340|343|346|

(1)已知声音在空气中的传播速度y(m/s)与气温x(℃)成一次函数关系,请求出该函数的表达式;
(2)若当日气温为8 ℃,小明观看到绚烂的烟花5 s后才听到声响,求小明与烟花之间的大致距离.
|气温/℃|0|5|10|15|20|25|
|声音在空气中的传播速度/(m/s)|331|334|337|340|343|346|

(1)已知声音在空气中的传播速度y(m/s)与气温x(℃)成一次函数关系,请求出该函数的表达式;
(2)若当日气温为8 ℃,小明观看到绚烂的烟花5 s后才听到声响,求小明与烟花之间的大致距离.
答案:
8.
(1)设函数表达式为y=kx+b(k≠0),将(0,331)和(10,337)代入,得{b=331,10k+b=337,解得{k=0.6,b=331,
∴y=0.6x+331.
(2)
∵当x=8时,y=0.6×8+331=335.8,
∴小明与烟花之间的大致距离为335.8×5=1679(m).
(1)设函数表达式为y=kx+b(k≠0),将(0,331)和(10,337)代入,得{b=331,10k+b=337,解得{k=0.6,b=331,
∴y=0.6x+331.
(2)
∵当x=8时,y=0.6×8+331=335.8,
∴小明与烟花之间的大致距离为335.8×5=1679(m).
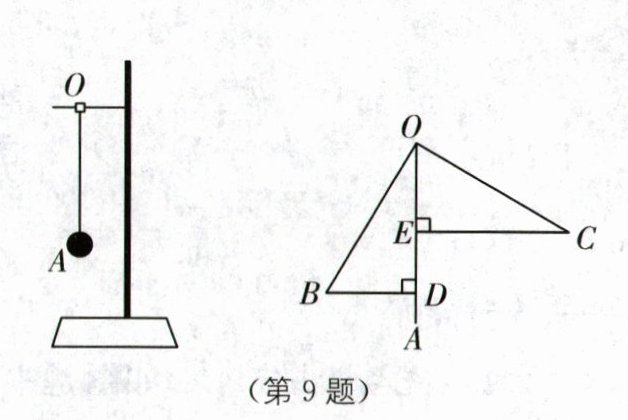
9.(2024·河北保定高阳期末改编)小明在物理课上学习了发声物体的振动实验后,对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A,小球A可以自由摆动,如图,OA表示小球静止时的位置.当小明用发声物体靠近小球时,小球从OA摆到OB位置,此时过点B作BD⊥OA于点D,当小球摆到OC位置时,OB与OC恰好垂直(图中的A,B,O,C在同一平面上),过点C作CE⊥OA于点E,测得CE= 15 cm,AD= 2 cm.
(1)试说明OE= BD;
(2)求OB的长.
(1)试说明OE= BD;
(2)求OB的长.

答案:
9.
(1)
∵OB⊥OC,
∴∠BOD+∠COE=90°.
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B.
在△COE和△OBD中,{∠CEO=∠ODB,∠COE=∠B,OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD.
(2)
∵△COE≌△OBD,
∴CE=OD=15 cm.
∵AD=2 cm,
∴OB=OA=OD+AD=17 cm.
(1)
∵OB⊥OC,
∴∠BOD+∠COE=90°.
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B.
在△COE和△OBD中,{∠CEO=∠ODB,∠COE=∠B,OC=BO,
∴△COE≌△OBD(AAS),
∴OE=BD.
(2)
∵△COE≌△OBD,
∴CE=OD=15 cm.
∵AD=2 cm,
∴OB=OA=OD+AD=17 cm.
查看更多完整答案,请扫码查看


