《2025年实验班提优大考卷八年级数学上册苏科版》

1.(2024·扬州中考)在平面直角坐标系中,点 P(1,2)关于坐标原点的对称点 P'的坐标为(A).
A.(-1,-2)
B.(-1,2)
C.(1,-2)
D.(1,2)

答案： A

2. 教材 P115 练习 T1·拓展 点 A 的坐标(x,y)满足$(x+3)^2+$|y+2|= 0,则点 A 的位置在(C).
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： C　[解析]
∵(x+3)²+|y+2|=0，
∴x+3=0，y+2=0，（几个非负数的和为0，则这几个非负数同时为0）
∴x=−3＜0，y=−2＜0，则点A在第三象限。故选C。

3. 变式提优→B 卷 T14 (2025·泰州泰兴期末)在平面直角坐标系中,点$ P(a^2+2,-2)$一定在(D).
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： D

4. 将点 P(-6,-9)向右平移 1 个单位,再向下平移 2 个单位后得到点 P',则点 P'的坐标为(D).
A.(-6,-8)
B.(-6,-11)
C.(-5,-9)
D.(-5,-11)

答案： D

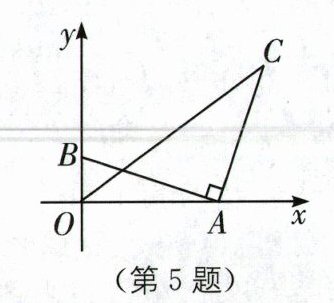
5.(2024·盐城东台一模)如图,在平面直角坐标系中,点 A(3,0),B(0,1),连接 AB,将线段 AB 绕点 A 顺时针旋转 90°得到线段 AC,连接 OC,则线段 OC 的长度为( ).

A.4
B.3√4
C.2√5
D.5

答案：
D　[解析]如图，作CH⊥x轴于点H。
∵A(3,0)，B(0,1)，
∴OA=3，OB=1。
∵∠AOB=∠BAC=∠AHC=90°，
∴∠BAO+∠HAC=90°，∠HAC+∠ACH=90°，
∴∠BAO=∠ACH。
∵AB=CA，
∴△ABO≌△CAH(AAS)，
∴AH=OB=1，CH=OA=3，
∴OH=OA+AH=3+1=4，
∴C(4,3)，
∴OC=√(OH²+CH²)=√(4²+3²)=5。故选D。

6.(山东淄博张店七中自主招生)点 A(4,3)经过某种图形变化后得到点 B(-3,4),这种图形变化可以是( ).

A.关于 x 轴对称
B.关于 y 轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°

答案：
C　[解析]如图，观察图形可知，点A绕点O逆时针旋转90°得到点B。故选C。

7. 变式提优→B 卷 T6 在平面直角坐标系中,点 A 的坐标为(-3,2),AB//x 轴,且 AB= 5,则点 B 的坐标为(B).
A.(-8,2)
B.(-8,2)或(2,2)
C.(-3,7)
D.(-3,7)或(-3,-3)

答案： B

8. 如图,在△AOB 中,OA= AB,顶点 A 的坐标为(3,4),底边 OB 在 x 轴上.将△AOB 绕点 B 按顺时针方向旋转一定角度后得△A'O'B,点 A 的对应点 A'在 x 轴上,则点 O'的坐标为( ).

A.(48/5,24/5)
B.(36/5,16/5)
C.(20/3,8√5/3)
D.(24/5,2√5)

答案：
A　[解析]如图，过点A作AG⊥x轴于点G，过点O'作O'H⊥x轴于点H。
∵点A的坐标为(3,4)，
∴OG=3，AG=4。在Rt△AOG中，由勾股定理，得OA=5。
∵OA=AB，
∴BG=OG=3，AB=OA=5。设BH=x，则A'H=5−x，在Rt△BO'H和Rt△A'O'H中，由勾股定理，得6²−x²=5²−(5−x)²，解得x=18/5，
∴OH=OB+BH=6+18/5=48/5。
∵S△OAB=S△O'A'B'，
∴OB·AG=BA'·O'H，
∴6×4=5O'H，
∴O'H=24/5，点O'的坐标为(48/5，24/5)。故选A

9. 教材 P131 复习题 T4·变式 在平面直角坐标系中,点 A(3,2)关于 x 轴的对称点为$ A_1,$将点$ A_1$向左平移 3 个单位得到点$ A_2,$则点$ A_2$的坐标为______(0,−2).

答案： (0,−2)

10. 在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)= (-a,b);②○(a,b)= (-a,-b);③Ω(a,b)= (a,-b).
按照以上变换例如:△(○(1,2))= (1,-2),则○(Ω(3,4))= (−3,4).

答案： (−3,4)