《2025年实验班提优大考卷八年级数学上册苏科版》

1. 变式提优→B 卷 T2 (2025·盐城东台期末)下列四组长度的线段中,可以构成直角三角形的三边长的是(B).
A.1,2,3
B.1.5,2,2.5
C.3,5,7
D.6,8,9

答案： B

2.(2025·南京秦淮区期末)下列各组数中,不是勾股数的是(C).
A.3,4,5
B.5,12,13
C.10,15,20
D.7,24,25

答案： C [解析]A.$3^{2}+4^{2}=5^{2}$,本组数是勾股数,不符合题意;B.$5^{2}+12^{2}=13^{2}$,本组数是勾股数,不符合题意;C.$10^{2}+15^{2}≠20^{2}$,本组数不是勾股数,符合题意;D.$7^{2}+24^{2}=25^{2}$,本组数是勾股数,不符合题意.故选 C.
易错警示 勾股数的定义:满足$a^{2}+b^{2}=c^{2}$的三个正整数称为勾股数.

3.(2025·河南洛阳西工区期中)如图,在4×4的正方形网格中,每个小正方形的边长都是1,点A,B,C都在小正方形的顶点上,则∠BAC的度数是(C).

A.30°
B.36°
C.45°
D.60°

答案： C

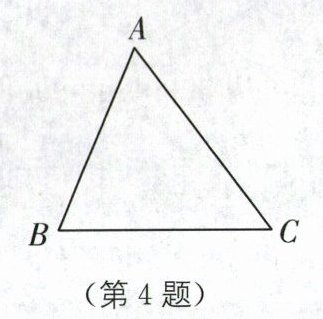
4. 传统文化《数书九章》(2023·南京中考)我国南宋数学家秦九韶的著作《数书九章》中有一道问题：“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里. 里法三百步,欲知为田几何？”问题大意：如图,在△ABC中,AB= 13里,BC= 14里,AC= 15里,则△ABC的面积是( ).

A.80 平方里
B.82 平方里
C.84 平方里
D.86 平方里

答案：
C [解析]如图,过点 A 作$AD⊥BC$于点 D.

设$BD=x$里,则$CD=(14 - x)$里.在$Rt△ABD$中,$AD^{2}=13^{2}-x^{2}$,在$Rt△ADC$中,$AD^{2}=15^{2}-(14 - x)^{2}$,$\therefore 13^{2}-x^{2}=15^{2}-(14 - x)^{2}$,解得$x = 5$.$\because$在$Rt△ACD$中,由勾股定理,得$AD = 12$里,$\therefore △ABC$的面积$=\frac{1}{2}BC\cdot AD=\frac{1}{2}×14×12 = 84$(平方里).故选 C.
归纳总结 本题考查了三角形面积、勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点.

5. 教材 P103 数学探究·变式 (2025·南京联合体期中)当n为正整数时,下列各组数：①3n,4n,5n；②$\frac{n}{3},\frac{n}{4},\frac{n}{5}$；③2n-1,2n+1,2n+3. 其中是勾股数的是(A).
A.①
B.①②
C.①③
D.②③

答案： A

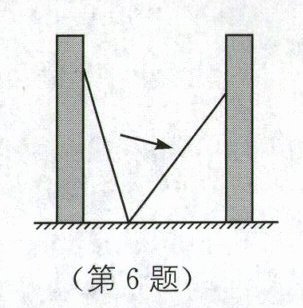
6.(2024·辽宁锦州期中)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米. 如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( ).

A.0.7 米
B.1.5 米
C.2.2 米
D.2.4 米

答案：
C [解析]如图,在$Rt△ACB$中,$\because ∠ACB = 90^{\circ },BC = 0.7$米,$AC = 2.4$米,$\therefore AB^{2}=0.7^{2}+2.4^{2}=6.25$.在$Rt△A'BD$中,$\because ∠A'DB = 90^{\circ },A'D = 2$米,$BD^{2}+A'D^{2}=A'B^{2}$,$\therefore BD^{2}+2^{2}=6.25$,$\therefore BD^{2}=2.25$.$\because BD ＞ 0$,$\therefore BD = 1.5$米,$\therefore CD = BC + BD = 0.7 + 1.5 = 2.2$(米).故选 C.

7. 传统文化《周髀算经》(2025·苏州工业园区期中)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载. 如图(1),以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图(2)的方式放置在最大正方形内. 则下列选项中一定正确的是(D).

A.$S_{阴影}= $直角三角形的面积
B.$S_{阴影}= S_{正方形①}$
C.$S_{阴影}= S_{正方形②}$
D.$S_{阴影}= $较小两个正方形重叠部分的面积

答案： D [解析]设直角三角形的斜边长为 c,较长直角边的长为 b,较短直角边的长为 a,由勾股定理得,$c^{2}=a^{2}+b^{2}$,$\therefore$阴影部分的面积$=c^{2}-b^{2}-a(c - b)=a^{2}-ac + ab = a(a + b - c)$,较小两个正方形重叠部分的宽$=a - (c - b)$,长 = a,则较小两个正方形重叠部分面积$=a(a + b - c)=$阴影部分的面积,因此知道图中阴影部分的面积等于较小两个正方形重叠部分的面积.故选 D.

8.(2025·山东东营经开区期中)下列命题：①如果a,b,c为一组勾股数,那么5a,5b,5c仍是勾股数；②如果直角三角形的两边长是3,4,那么另一边必是5；③如果一个三角形的三边长是5,13,14,那么此三角形必是直角三角形；④如果一个等腰直角三角形的三边长是a,b,c(a＞b= c),那么$a^{2}:b^{2}:c^{2}= 2:1:1$. 其中正确的是(A).
A.①④
B.①③
C.①②
D.②④

答案： A [解析]①设$a^{2}+b^{2}=c^{2}$,$\because (5a)^{2}+(5b)^{2}=25a^{2}+25b^{2}=25(a^{2}+b^{2})=25c^{2}=(5c)^{2}$,而 5a,5b,5c 一定是正整数,勾股数是一组正整数$\therefore 5a,5b,5c$仍是勾股数,故①符合题意;②如果直角三角形的两边长是 3,4,则另一边的长可能为$\sqrt{4^{2}-3^{2}}=\sqrt{7}$,且符合三角形的两边之和大于第三边,故②不符合题意;③$5^{2}+13^{2}=25 + 169 = 194≠14^{2}$,故③不符合题意;④$\because$一个等腰直角三角形的三边长 a,b,c 满足$a ＞ b = c$,$\therefore a^{2}=b^{2}+c^{2}=b^{2}+b^{2}=2b^{2}=2c^{2}$,即$a^{2}:b^{2}:c^{2}=2:1:1$,故④符合题意.故选 A.
归纳总结 本题主要考查了勾股数和直角三角形的性质,正确掌握勾股数的定义和直角三角形的性质是解题的关键.