第99页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
8. (2022·青羊)甲、乙两人沿同一条路从$A$地出发,去往$100\ km外的B$地,甲、乙两人离$A地的距离s(km)与时间t(h)$之间的关系如图所示,以下说法正确的是(
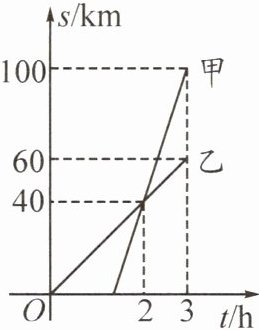
A.甲的速度是$60\ \text{km/h}$
B.乙的速度是$30\ \text{km/h}$
C.甲、乙同时到达$B$地
D.甲出发$2\ \text{h}$后两人第一次相遇
A
)
A.甲的速度是$60\ \text{km/h}$
B.乙的速度是$30\ \text{km/h}$
C.甲、乙同时到达$B$地
D.甲出发$2\ \text{h}$后两人第一次相遇
答案:
A
9. (1)(2025·编写)某单位今年“十一”期间要组团去北京旅游,与旅行社联系时,甲旅行社提出每人次收$300$元车费和住宿费,不优惠;乙旅行社提出每人次收$350$元车费和住宿费,但有$3$人可享受免费待遇.
①分别写出甲、乙两旅行社的收费与旅行人数之间的函数关系式;
②如果组织$20$人的旅行团时,选哪家旅行社比较合算?当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
(2)(2022·武侯)由于全球汽车芯片短缺,汽车生产成本增加,某汽车生产厂商计划提高汽车出厂价格,据市场反馈,某型号汽车出厂价格为$8$万元/辆时,其月销量为$2000$辆,且出厂价格每提高$1$万元/辆,月销量将减少$300$辆,设该型号汽车每辆出厂价格为$x(x > 8)$万元时,其月销量为$y$辆.
①求$y与x$之间的函数关系式;
②若汽车生产商计划该型号汽车的月销量不少于$1400$辆,在①的基础上,请根据函数中$y的值随x$值的变化而变化的特点,求该型号汽车的出厂价格最多应定为每辆多少万元.
①分别写出甲、乙两旅行社的收费与旅行人数之间的函数关系式;
②如果组织$20$人的旅行团时,选哪家旅行社比较合算?当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
(2)(2022·武侯)由于全球汽车芯片短缺,汽车生产成本增加,某汽车生产厂商计划提高汽车出厂价格,据市场反馈,某型号汽车出厂价格为$8$万元/辆时,其月销量为$2000$辆,且出厂价格每提高$1$万元/辆,月销量将减少$300$辆,设该型号汽车每辆出厂价格为$x(x > 8)$万元时,其月销量为$y$辆.
①求$y与x$之间的函数关系式;
②若汽车生产商计划该型号汽车的月销量不少于$1400$辆,在①的基础上,请根据函数中$y的值随x$值的变化而变化的特点,求该型号汽车的出厂价格最多应定为每辆多少万元.
答案:
(1)[解]①甲旅行社:$y = 300x$.
乙旅行社:$x\leqslant3$时,$y = 350x$;$x > 3$时,$y = 350(x - 3) = 350x - 1050$.
②当$x = 20$时,甲旅行社:$y = 300×20 = 6000$(元),乙旅行社:$y = 350×20 - 1050 = 5950$(元).
因为$5950<6000$,所以选乙旅行社合算.
由$300x = 350x - 1050$,解得$x = 21$.
故当旅行团为$21$人时,选甲或乙旅行社所需费用一样多.
(2)[解]①依题意,得$y = 2000 - 300(x - 8)$,即$y = - 300x + 4400(x > 8)$.
②(方法一)依题意,得$- 300x + 4400\geqslant1400$,解得$x\leqslant10$.
答:该型号汽车的出厂价格最多应定为每辆$10$万元.
(方法二)因为$k = - 300<0$,所以$y$随$x$的增大而减小.
又因为$y\geqslant1400$,所以当$y$取得最小值时,$x$取得最大值.
当$y = 1400$时,$- 300x + 4400 = 1400$,解得$x = 10$,所以该型号汽车的出厂价格最多应定为每辆$10$万元.
(1)[解]①甲旅行社:$y = 300x$.
乙旅行社:$x\leqslant3$时,$y = 350x$;$x > 3$时,$y = 350(x - 3) = 350x - 1050$.
②当$x = 20$时,甲旅行社:$y = 300×20 = 6000$(元),乙旅行社:$y = 350×20 - 1050 = 5950$(元).
因为$5950<6000$,所以选乙旅行社合算.
由$300x = 350x - 1050$,解得$x = 21$.
故当旅行团为$21$人时,选甲或乙旅行社所需费用一样多.
(2)[解]①依题意,得$y = 2000 - 300(x - 8)$,即$y = - 300x + 4400(x > 8)$.
②(方法一)依题意,得$- 300x + 4400\geqslant1400$,解得$x\leqslant10$.
答:该型号汽车的出厂价格最多应定为每辆$10$万元.
(方法二)因为$k = - 300<0$,所以$y$随$x$的增大而减小.
又因为$y\geqslant1400$,所以当$y$取得最小值时,$x$取得最大值.
当$y = 1400$时,$- 300x + 4400 = 1400$,解得$x = 10$,所以该型号汽车的出厂价格最多应定为每辆$10$万元.
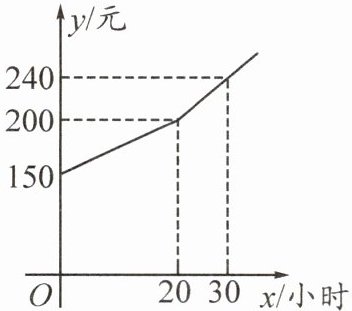
10. (1)(2025·编写)为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为$x$小时,该月可得(即下月他可获得)的总费用为$y$元,则$y$(元)和$x$(小时)之间的函数图象如图所示.
①根据图象,请你写出小强每月的基本生活费;父母是如何奖励小强做家务劳动的?
②若小强希望$2月份有300$元费用,则小强$1$月份需做家务多长时间?
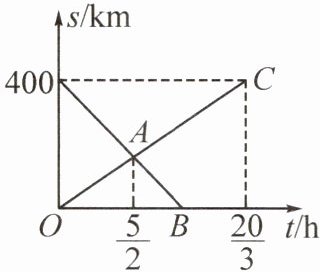
(2)(2022·双流)一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车距乙地的路程$s(\text{km})与行驶时间t(\text{h})$的关系如图所示,请解答下列问题:
①求点$A$的坐标;
②求线段$AB所表示的s与t$之间的函数关系式.
①根据图象,请你写出小强每月的基本生活费;父母是如何奖励小强做家务劳动的?
②若小强希望$2月份有300$元费用,则小强$1$月份需做家务多长时间?

(2)(2022·双流)一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,两车距乙地的路程$s(\text{km})与行驶时间t(\text{h})$的关系如图所示,请解答下列问题:
①求点$A$的坐标;
②求线段$AB所表示的s与t$之间的函数关系式.

答案:
(1)[解]①小强父母给小强的每月基本生活费为$150$元.
如果小强每月家务劳动时间不超过$20$小时,每小时获奖励$2.5$元;如果小强每月家务劳动时间超过$20$小时,那么$20$小时按每小时$2.5$元奖励,超过部分按每小时$4$元奖励.
②设$x\geqslant20$时$y$与$x$的函数关系式为$y = kx + b$,
则$\begin{cases}200 = 20k + b\\240 = 30k + b\end{cases}$,解得$\begin{cases}k = 4\\b = 120\end{cases}$,所以$y = 4x + 120$.
由题意得$4x + 120 = 300$,解得$x = 45$.
答:当小强$1$月份家务劳动时间为$45$小时时,$2$月份得到的费用为$300$元.
(2)[解]①由图象,可得慢车的速度为$400÷\frac{20}{3} = 60(km/h)$.
因为点$A$的意义为慢车行驶$\frac{5}{2}h$,距离乙地的路程,所以$60×\frac{5}{2} = 150(km)$,所以点$A$的坐标为$(\frac{5}{2},150)$.
②设线段$AB$对应的函数解析式为$s = kt + b$,
由图象可得$AB$经过点$(0,400)$和$(\frac{5}{2},150)$,
所以$\begin{cases}b = 400\frac{5}{2}k + b = 150\end{cases}$,解得$\begin{cases}k = - 100\\b = 400\end{cases}$,
即线段$AB$对应的函数解析式为$s = - 100t + 400$.
当$s = 0$时,$0 = - 100t + 400$,解得$t = 4$,
所以线段$AB$所表示的$s$与$t$之间的函数关系式为$s = - 100t + 400(\frac{5}{2}\leqslant t\leqslant4)$.
(1)[解]①小强父母给小强的每月基本生活费为$150$元.
如果小强每月家务劳动时间不超过$20$小时,每小时获奖励$2.5$元;如果小强每月家务劳动时间超过$20$小时,那么$20$小时按每小时$2.5$元奖励,超过部分按每小时$4$元奖励.
②设$x\geqslant20$时$y$与$x$的函数关系式为$y = kx + b$,
则$\begin{cases}200 = 20k + b\\240 = 30k + b\end{cases}$,解得$\begin{cases}k = 4\\b = 120\end{cases}$,所以$y = 4x + 120$.
由题意得$4x + 120 = 300$,解得$x = 45$.
答:当小强$1$月份家务劳动时间为$45$小时时,$2$月份得到的费用为$300$元.
(2)[解]①由图象,可得慢车的速度为$400÷\frac{20}{3} = 60(km/h)$.
因为点$A$的意义为慢车行驶$\frac{5}{2}h$,距离乙地的路程,所以$60×\frac{5}{2} = 150(km)$,所以点$A$的坐标为$(\frac{5}{2},150)$.
②设线段$AB$对应的函数解析式为$s = kt + b$,
由图象可得$AB$经过点$(0,400)$和$(\frac{5}{2},150)$,
所以$\begin{cases}b = 400\frac{5}{2}k + b = 150\end{cases}$,解得$\begin{cases}k = - 100\\b = 400\end{cases}$,
即线段$AB$对应的函数解析式为$s = - 100t + 400$.
当$s = 0$时,$0 = - 100t + 400$,解得$t = 4$,
所以线段$AB$所表示的$s$与$t$之间的函数关系式为$s = - 100t + 400(\frac{5}{2}\leqslant t\leqslant4)$.
查看更多完整答案,请扫码查看


