《2025年天府前沿八年级数学上册北师大版》

10. (1)(2025·编写)近似计算：
①估算$\sqrt{43}$的大小(误差小于 0.1)；
②求$\sqrt{3}$的近似值(精确到 0.1)。
(2)(2025·编写)一块正方形瓷砖的面积为$50cm^2$,求它的边长(精确到$0.1cm$)。

答案：
(1)[解]①
∵ 36 ＜ 43 ＜ 49，
∴ 6 ＜ $\sqrt { 43 }$ ＜ 7，
∴ $\sqrt { 43 }$ 的整数部分是 6．
∵ 6.5² = 42.25，6.6² = 43.56，
∴ 6.5 ＜ $\sqrt { 43 }$ ＜ 6.6，
∴ $\sqrt { 43 }$ ≈ 6.5 或 $\sqrt { 43 }$ ≈ 6.6．
②
∵ 1 ＜ 3 ＜ 4，
∴ 1 ＜ $\sqrt { 3 }$ ＜ 2．又
∵ 1.7² = 2.89，1.8² = 3.24，
∴ 1.7² ＜ 3 ＜ 1.8²，
∴ 1.7 ＜ $\sqrt { 3 }$ ＜ 1.8．又
∵ 1.73² = 2.9929，1.74² = 3.0276，
∴ 1.73² ＜ 3 ＜ 1.74²，
∴ 1.73 ＜ $\sqrt { 3 }$ ＜ 1.74，
∴ $\sqrt { 3 }$ ≈ 1.7．
(2)[解]设正方形瓷砖的边长为 a cm，则 a² = 50，
∴ a = ± $\sqrt { 50 }$．
∵ 正方形的边长 a ＞ 0，
∴ a = $\sqrt { 50 }$ = 5 $\sqrt { 2 }$．又
∵ 49 ＜ 50 ＜ 64，即 7 ＜ 5 $\sqrt { 2 }$ ＜ 8，
∴ 7 ＜ a ＜ 8．
∵ 7² = 49，7.1² = 50.41，
∴ $\sqrt { 50 }$ ≈ 7.1．故正方形瓷砖的边长约为 7.1 cm．

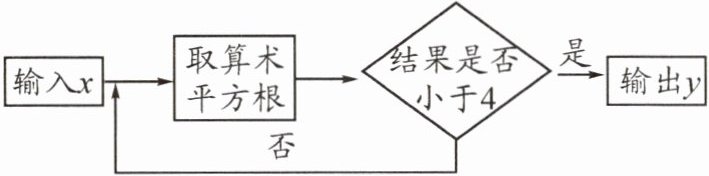
11. (2025·青羊)如图是一个数值转换机示意图,当输入$x$的值为 100 时,输出$y$的值为$\sqrt { 10 }$。

答案： $\sqrt { 10 }$

12. (2025·天府新区)我们用符号$[x]$表示一个不大于实数x的最大的整数,如：$[2.78]= 2$,$[-0.23]= -1$,则按这个规律,$[-1-\sqrt{7}]=$-4。

答案： -4

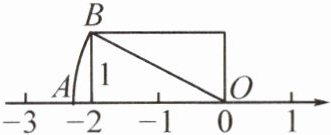
13. (2025·编写)如图,已知$OA = OB$,若点$A对应的数是a$,则$a与-\frac{5}{2}的大小关系是a$＞$-\frac{5}{2}$。

答案： ＞

14. (2024·高新)已知数$a的平方根为2x + 1和1 - 7x$,$\sqrt{17}的整数部分为b$。
(1)求$a$,$b$的值；
(2)若$\sqrt{17}的小数部分为c$,求$25a-(b + c)^2$的平方根。

答案： [解]
(1)
∵ 实数 a 的平方根为 2x + 1，1 - 7x，
∴ 2x + 1 + 1 - 7x = 0，解得 x = $\frac { 2 } { 5 }$，
∴ 2x + 1 = $\frac { 9 } { 5 }$，
∴ a = ( $\frac { 9 } { 5 }$ )² = $\frac { 81 } { 25 }$．
∵ 16 ＜ 17 ＜ 25，
∴ 4 ＜ $\sqrt { 17 }$ ＜ 5，
∴ b = 4．
(2)
∵ 4 ＜ $\sqrt { 17 }$ ＜ 5，
∴ c = $\sqrt { 17 }$ - 4．
∵ a = $\frac { 81 } { 25 }$，b = 4，
∴ 25a - (b + c)² = 25× $\frac { 81 } { 25 }$ - (4 + $\sqrt { 17 }$ - 4)² = 81 - 17 = 64，
∴ 25a - (b + c)² 的平方根为 ±8．

15. (2024·天府新区)如图,线段$AB$的长度为 5,点$P$,$M为线段AB$外两动点,且$PA = 4$,$PM = PB$,$\angle BPM = 90^{\circ}$,求线段$AM$长的最大值。

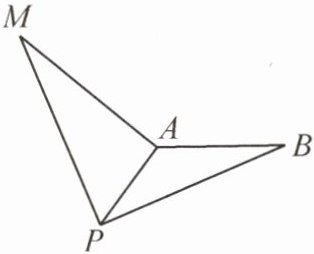
答案：
[解]如图，由题意知，PM = PB，∠BPM = 90°，将△PMA绕着点P顺时针旋转90°得到△PBN，连接AN，则△APN是等腰直角三角形，
∴PN = PA = 4，BN = AM．

∵AB = 5，
∴线段AM长的最大值 = 线段BN长的最大值，
∴当N在线段BA的延长线上时，线段BN的长取得最大值，最大值 = AB + AN．
∵△APN是等腰直角三角形，
∴AN = $\sqrt { 2 }$AP = 4 $\sqrt { 2 }$，
∴线段AM长的最大值为 4 $\sqrt { 2 }$ + 5．