《2025年天府前沿八年级数学上册北师大版》

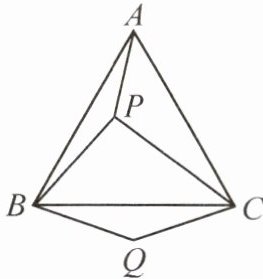
10. (2025·编写)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ = 60°,且BQ = BP,连接CQ。
(1)求证：AP = CQ；
(2)若PA：PB：PC = 3：4：5,连接PQ,求证：△PQC是直角三角形。

答案：
[证明]
(1)$\because \triangle ABC$ 是等边三角形，
$\therefore \angle ABC = 60^{\circ}$，$AB = BC$，
$\therefore \angle ABP + \angle PBC = 60^{\circ}$.
又 $\because \angle PBQ = 60^{\circ}$，

$\therefore \angle QBC + \angle PBC = 60^{\circ}$，
$\therefore \angle ABP = \angle QBC$.
又 $\because AB = BC$，$BP = BQ$，
$\therefore \triangle ABP \cong \triangle CBQ(SAS)$，$\therefore AP = CQ$.
(2)由 $PA:PB:PC = 3:4:5$，
可设 $PA = 3a$，$PB = 4a$，$PC = 5a$.
如图，连接 $PQ$，
在 $\triangle PBQ$ 中，由于 $PB = BQ = 4a$，且 $\angle PBQ = 60^{\circ}$，
$\therefore \triangle PBQ$ 为等边三角形.
$\therefore PQ = 4a$.
在 $\triangle PQC$ 中，
$\because PQ^{2} + QC^{2} = 16a^{2} + 9a^{2} = 25a^{2} = PC^{2}$，
$\therefore \triangle PQC$ 是直角三角形.

11. (2025·编写)某中学要举办运动会,现需装饰一根高为9米,底面半径为$\frac{2}{\pi}$米的圆柱。如图,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根彩带(宽度不计)从点A顺着圆柱侧面绕3圈到达点B,那么这根彩带的长度最短是15 米。

答案： 15 米

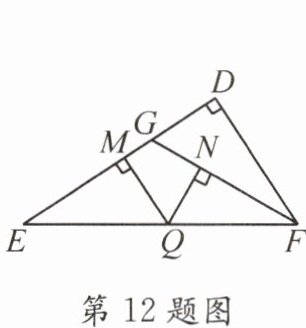
12. (2025·编写)如图,在△DEF中,∠D = 90°,DG：GE = 1：3,GE = GF,Q是EF上一动点,过点Q作QM⊥DE于点M,QN⊥GF于点$N,EF^2 = 192,$则QM + QN的值是______8。

答案： 8

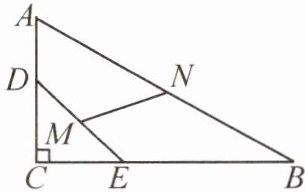
13. (2025·编写)如图,在△ABC中,∠ACB = 90°,AC = 6,BC = 8,线段DE的长是5,且两个端点D,E分别在边AC,BC上滑动,点M,N分别是DE,AB的中点,则MN的最小值为______2.5。

答案： 2.5

14. (2025·编写)如图,AB = AC = 4,P是BC上异于B,C的一点,求$AP^2 + BP·PC$的值。

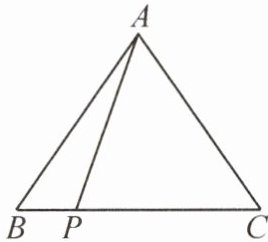
答案：
[解]如图，过点 $A$ 作 $AD \perp BC$ 于点 $D$.

$\because AD \perp BC$，$\therefore \triangle ADP$ 与 $\triangle ABD$ 都为直角三角形.
$\therefore AP^{2} = AD^{2} + DP^{2}$，$AB^{2} = AD^{2} + BD^{2}$.
$\because AB = AC$，$AD \perp BC$，$\therefore BD = CD$.
$\because PC = CD + DP$，$\therefore PC = BD + DP$.
$\because BP = BD - DP$，
$\therefore BP \cdot PC = BD^{2} - DP^{2}$.
$\therefore AP^{2} + BP \cdot PC = AD^{2} + BD^{2} = AB^{2}$.
$\because AB = 4$，$\therefore AP^{2} + BP \cdot PC = 16$.

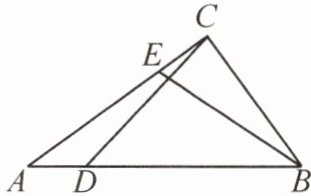
15. (2025·郫都)如图,在△ABC中,∠ABC = 60°,BC = 8,AC = 10,点D,E分别在AB,AC边上,且AD = CE,求$(CD + BE)^2$的最小值。

答案：
[解]如图，作 $CK // AB$，使得 $CK = CA$. 作 $BG \perp KC$ 交 $KC$ 的延长线于点 $G$，连接 $BK$，$KE$.

$\because CK // AB$，$\therefore \angle KCE = \angle A$.
又 $\because CK = CA$，$CE = AD$，
$\therefore \triangle CKE \cong \triangle ACD(SAS)$，$\therefore KE = CD$.
$\because CD + BE = EK + EB \geq BK$，
$\therefore CD + BE$ 的最小值为 $BK$ 的长.
在 $Rt\triangle BCG$ 中，$\because \angle G = 90^{\circ}$，$\angle BCG = \angle ABC = 60^{\circ}$，$BC = 8$，
$\therefore CG = \frac{1}{2}BC = 4$，$BG^{2} = 48$，
$\therefore GK = CG + CK = 4 + 10 = 14$.
在 $Rt\triangle KBG$ 中，$BK^{2} = GK^{2} + BG^{2} = 14^{2} + 48 = 244$.
$\therefore (CD + BE)^{2}$ 的最小值为 244.