《2025年天府前沿八年级数学上册北师大版》

9. (1)(2025·编写)把下列各数填在相应的大括号内.
$\frac {π}{2}$,$-|-3|$,$0$,$\frac {22}{7}$,$-3.1$,$1.1010010001…$(相邻两个$1之间0的个数依次多1$).
整数：…$\{ $$-|-3|,0$$\}$；
分数：…$\{ $$\frac{22}{7}, - 3.1$$\}$；
无理数：…$\{ $$\frac {π}{2},1.1010010001…$(相邻两个1之间0的个数依次多1)$\}$.
(2)(2025·编写)有四张不透明的卡片$\boxed{2}$,$\boxed{\frac {22}{7}}$,$\boxed{π}$,$\boxed{\frac {π}{2}}$,除正面的数不同外,其余都相同,将其背面朝上洗匀后,从中随机抽取一张卡片,抽到写有无理数卡片的概率为多少？
因为无理数有两个，所以抽到无理数卡片的概率是$\frac{2}{4} = \frac{1}{2}$.

答案：
(1)[解]整数:$\{ -|-3|,0…\}$;
分数:$\{ \frac{22}{7}, - 3.1…\}$;
无理数:$\{ \frac{π}{2},1.1010010001…$(相邻两个1之间0的个数依次多1)$…\}$.
(2)[解]因为无理数有两个，所以抽到无理数卡片的概率是$\frac{2}{4} = \frac{1}{2}$.

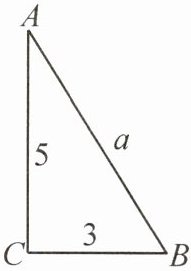
10. (1)(2025·编写)如图,一个直角三角形两条直角边的长分别是$3和5$,则斜边的长$a$是有理数吗？

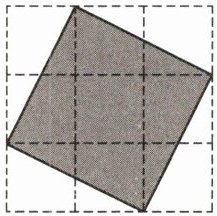
(2)(2025·编写)如图,在$3×3$的方格中,有一阴影正方形,设每一个小方格的边长为$1$. 请解答下面的问题：
①阴影正方形的面积是多少？
②阴影正方形的边长介于哪两个整数之间？

答案：
(1)[解]由勾股定理得$a^{2}=34$.因为34不是完全平方数，所以a不是有理数.
(2)[解]①阴影正方形的面积是5.
②设阴影正方形的边长为a，
则由①知$a^{2}=5$.
因为$2^{2}＜a^{2}＜3^{2}$，所以$2 ＜ a ＜ 3$.
故它的边长介于2和3之间.

11. (1)(2025·编写)下列各式中的$x$是无理数的有③(填序号).
①$5x^{2}= 45$；②$3x-5= 0$；③$x^{3}= 9$；④$7x-3= 5$.
(2)(2025·编写)有五个数：$0.123$,$(-1.5)^{3}$,$3.1416$,$-2π$,$0.1020020002…$(相邻两个$2之间0的个数逐次加1$),若其中无理数的个数为$x$,整数的个数为$y$,非负数的个数为$z$,则$x+y+z= $5.

答案：
(1)③　
(2)5

12. (2025·编写)有下列说法：
①无限小数都是无理数；
②无理数是无限不循环的小数；
③无理数包括正无理数、$0$、负无理数；
④无理数都可以用数轴上的点来表示.
其中正确说法的个数是____2.

答案： 2