《2025年天府前沿八年级数学上册北师大版》

7. (2024·成华)中国象棋文化历史悠久。如图是某次对弈的残图,若在图中建立平面直角坐标系,使棋子“帅”位于点$(-2,-1)$的位置,则经过棋子“帅”和“马”所在的点的一次函数表达式为(C)
A.$y = 2x + 1$
B.$y = 2x - 1$
C.$y = x + 1$
D.$y = x - 1$

答案： C

8. (2025·编写)如图,直线$y = kx(k\neq0)与y = \frac{2}{3}x + 2在第二象限交于点A$,直线$y = \frac{2}{3}x + 2分别交x$轴、$y轴于B$,$C$两点,若$3S_{\triangle ABO} = S_{\triangle BOC}$,则方程组$\begin{cases}kx - y = 0,\\2x - 3y = -6\end{cases} $的解为(C)
A.$\begin{cases}x = -1\\y = \frac{4}{3}\end{cases} $
B.$\begin{cases}x = -\frac{3}{2}\\y = 1\end{cases} $
C.$\begin{cases}x = -2\\y = \frac{2}{3}\end{cases} $
D.$\begin{cases}x = -\frac{3}{4}\\y = \frac{3}{2}\end{cases} $

答案： C

9. (1)(2025·编写)已知$y - 1与2x + 3$成正比例,且当$x = -\frac{5}{3}$时,$y = 0$,求$y关于x$的函数解析式。
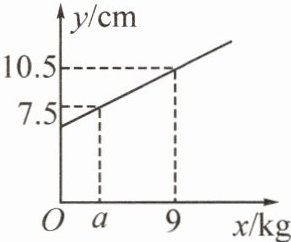
(2)(2025·编写)如图,一个弹簧不挂重物时长$6cm$,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比,弹簧总长$y$(单位：$cm$)关于所挂物体质量$x$(单位：$kg$)的函数图象如图所示,求图中$a$的值。

答案：
(1)【解】设 $ y - 1 = k(2x + 3)(k \neq 0) $，把 $ x = -\frac{5}{3} $，$ y = 0 $ 代入上式，得 $ -1 = (-\frac{10}{3} + 3)k $，解得 $ k = 3 $，
所以 $ y - 1 = 3(2x + 3) $，即 $ y = 6x + 10 $。
(2)【解】设 $ y $ 与 $ x $ 的函数关系式为 $ y = kx + b $，将点 $ (0,6) $，$ (9,10.5) $ 代入上式，得 $ \begin{cases} b = 6, \\ 9k + b = 10.5, \end{cases} $
解得 $ \begin{cases} k = 0.5, \\ b = 6, \end{cases} $
即 $ y $ 与 $ x $ 的函数关系式是 $ y = 0.5x + 6 $。
当 $ y = 7.5 $ 时，$ 7.5 = 0.5x + 6 $，解得 $ x = 3 $，即 $ a $ 的值为 3。

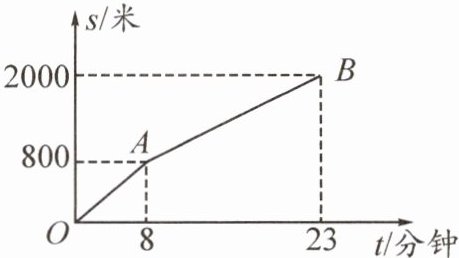
10. (1)(2025·编写)小明从家步行到学校需走的路程为$2000$米。图中的折线$OAB反映了小明从家步行到学校所走的路程s$(米)与时间$t$(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行$20$分钟时,距离学校还有多少米？

(2)(2025·温江)暑假期间,小明和父母一起开车到距家$200$千米的景点旅游。出发前,汽车油箱内储油$45$升；当行驶$150$千米时,发现油箱剩余油量为$30$升。
①已知油箱内剩余油量$y$(升)是行驶路程$x$(千米)的一次函数,求$y与x$之间的函数关系式；
②当油箱中剩余油量少于$3$升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家？请说明理由。

答案：
(1)【解】设线段 $ AB $ 对应的函数解析式为 $ s = kt + b $，
则有 $ \begin{cases} 8k + b = 800, \\ 23k + b = 2000, \end{cases} $ 解得 $ \begin{cases} k = 80, \\ b = 160, \end{cases} $
即线段 $ AB $ 对应的函数解析式为 $ s = 80t + 160 $。
当 $ t = 20 $ 时，$ s = 80 × 20 + 160 = 1760 $，
$ 2000 - 1760 = 240 $（米），
即当小明从家出发去学校步行 20 分钟时，距离学校还有 240 米。
(2)【解】①设 $ y = kx + b $。
由题意知，当 $ x = 0 $ 时，$ y = 45 $，当 $ x = 150 $ 时，$ y = 30 $，
$ \therefore \begin{cases} b = 45, \\ 150k + b = 30, \end{cases} $ 解得 $ \begin{cases} k = -\frac{1}{10}, \\ b = 45, \end{cases} $
$ \therefore y $ 与 $ x $ 之间的函数关系式为 $ y = -\frac{1}{10}x + 45(0 \leq x \leq 450) $。
②能。理由如下：
当 $ x = 400 $ 时，$ y = -\frac{1}{10} × 400 + 45 = 5 ＞ 3 $，$ \therefore $ 他们能在汽车报警前回到家。