第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
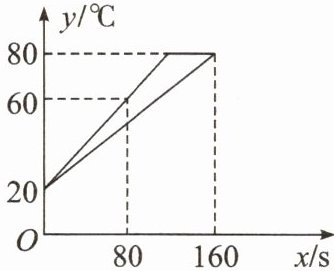
9. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量、相同温度的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系.根据记录的数据画出的函数图象如图所示.
(1)加热前水温是
(2)求乙壶的水温y关于加热时间x的函数解析式.
(3)当甲壶的水温刚达到80℃时,乙壶的水温是
(1)加热前水温是
20
℃.(2)求乙壶的水温y关于加热时间x的函数解析式.
(3)当甲壶的水温刚达到80℃时,乙壶的水温是
65
℃.
(2)设乙壶的水温y关于加热时间x的函数关系式为$ y=kx+b(k≠0) $,将(0,20),(160,80)代入$ y=kx+b $,得$ 20=b $,$ 80=160k+b $,解得$ k=\frac{3}{8} $,所以乙壶的水温y关于加热时间x的函数解析式为$ y=\frac{3}{8}x+20 $。
答案:
解:
(1)因为当x=0时,y=20,所以加热前水温是$ 20^{\circ}C $.故答案为20.
(2)设乙壶的水温y关于加热时间x的函数关系式为$ y=kx+b(keq 0) $,将(0,20),(160,80)代入$ y=kx+b $,得$ 20=b $,$ 80=160k+b $,$ k=\frac{3}{8} $,所以$ y=\frac{3}{8}x+20 $.
(3)甲壶的加热速度为$ (60-20)÷ 80=\frac{1}{2}(^{\circ}C/s) $,当甲水壶的温度为$ 80^{\circ}C $时,加热时间为$ (80-20)÷ \frac{1}{2}=120(s) $,将$ x=120 $代入$ y=\frac{3}{8}x+20 $,得$ y=65 $.故答案为65.
(1)因为当x=0时,y=20,所以加热前水温是$ 20^{\circ}C $.故答案为20.
(2)设乙壶的水温y关于加热时间x的函数关系式为$ y=kx+b(keq 0) $,将(0,20),(160,80)代入$ y=kx+b $,得$ 20=b $,$ 80=160k+b $,$ k=\frac{3}{8} $,所以$ y=\frac{3}{8}x+20 $.
(3)甲壶的加热速度为$ (60-20)÷ 80=\frac{1}{2}(^{\circ}C/s) $,当甲水壶的温度为$ 80^{\circ}C $时,加热时间为$ (80-20)÷ \frac{1}{2}=120(s) $,将$ x=120 $代入$ y=\frac{3}{8}x+20 $,得$ y=65 $.故答案为65.
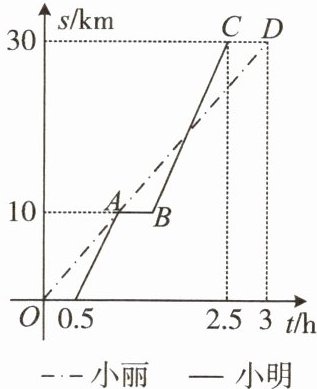
10. 小明和小丽骑车去山庄游玩,小明比小丽晚出发0.5 h,追上小丽后休息了一段时间,继续以相同的速度骑行.他们离出发点的路程s(km)关于时间t(h)的变化情况如图所示.
(1)分别求出小丽和小明骑行的速度.
(2)求线段BC所在直线的函数关系式.
(3)小明第2次追上小丽时,求他们距离山庄的路程.
(1)分别求出小丽和小明骑行的速度.
(2)求线段BC所在直线的函数关系式.
(3)小明第2次追上小丽时,求他们距离山庄的路程.

答案:
解:
(1)小丽骑行的速度为$ 30÷ 3=10(km/h) $,$ 10÷ 10=1(h) $,
∴点A为(1,10),小明骑行的速度为$ 10÷ (1-0.5)=20(km/h) $.答:小丽骑行的速度为10 km/h,小明骑行的速度为20 km/h.
(2)$ (30-10)÷ 20=1(h) $,$ 2.5-1=1.5(h) $,
∴点B为(1.5,10),$ s=10+20(t-1.5)=20t-20 $,
∴线段BC所在直线的函数关系式为$ s=20t-20(1.5\leq t\leq 2.5) $.
(3)线段OD所在直线的函数关系式$ s=10t(0\leq t\leq 3) $,当小明第2次追上小丽时,由$ 10t=20t-20 $,解得$ t=2 $,$ 30-2× 10=10(km) $.答:小明第2次追上小丽时,他们距离山庄的路程为10 km.
(1)小丽骑行的速度为$ 30÷ 3=10(km/h) $,$ 10÷ 10=1(h) $,
∴点A为(1,10),小明骑行的速度为$ 10÷ (1-0.5)=20(km/h) $.答:小丽骑行的速度为10 km/h,小明骑行的速度为20 km/h.
(2)$ (30-10)÷ 20=1(h) $,$ 2.5-1=1.5(h) $,
∴点B为(1.5,10),$ s=10+20(t-1.5)=20t-20 $,
∴线段BC所在直线的函数关系式为$ s=20t-20(1.5\leq t\leq 2.5) $.
(3)线段OD所在直线的函数关系式$ s=10t(0\leq t\leq 3) $,当小明第2次追上小丽时,由$ 10t=20t-20 $,解得$ t=2 $,$ 30-2× 10=10(km) $.答:小明第2次追上小丽时,他们距离山庄的路程为10 km.
11. 某共享单车租赁公司为缓解暑假期间及假期后的交通压力,鼓励市民绿色出行,特推出以下优惠活动:
①优惠卡:月租费为15元,每次凭卡号用车5折优惠;
②月卡:月租费为m元,凭卡号用车不再收取费用.
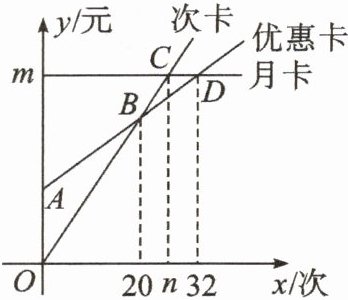
以上两种优惠活动在元旦前均有效,不限次数,同时普通用车业务正常办理,每次用车不超过30分钟收费1.5元(记作次卡).一位市民每次出行用车均不超过30分钟,设每月用车次数为x次,所需费用为y元.在同一平面直角坐标系中,3种计费方式对应的函数图象如图所示.
(1)分别求出m,n的值及选择次卡和优惠卡时y与x的函数关系式.
(2)请根据函数图象判断,选择哪种计费方式合算.
①优惠卡:月租费为15元,每次凭卡号用车5折优惠;
②月卡:月租费为m元,凭卡号用车不再收取费用.
以上两种优惠活动在元旦前均有效,不限次数,同时普通用车业务正常办理,每次用车不超过30分钟收费1.5元(记作次卡).一位市民每次出行用车均不超过30分钟,设每月用车次数为x次,所需费用为y元.在同一平面直角坐标系中,3种计费方式对应的函数图象如图所示.
(1)分别求出m,n的值及选择次卡和优惠卡时y与x的函数关系式.
(2)请根据函数图象判断,选择哪种计费方式合算.

答案:
解:
(1)次卡对应的函数关系式为$ y_{1}=1.5x(x\geq 0) $,将$ x=20 $代入$ y_{1}=1.5x $,可得$ y_{1}=30 $,所以点B的坐标为(20,30).设优惠卡对应的函数关系式为$ y_{2}=kx+b(x\geq 0) $,将A(0,15),B(20,30)代入$ y_{2}=kx+b $,得$ b=15 $,$ 20k+b=30 $,$ k=0.75 $,所以优惠卡对应的函数关系式为$ y_{2}=0.75x+15(x\geq 0) $.将D(32,m)代入$ y_{2}=0.75x+15 $,可得$ m=39 $,将C(n,39)代入$ y_{1}=1.5x $,可得$ n=26 $,所以$ m=39 $,$ n=26 $.选择次卡时y与x的函数关系式为$ y=1.5x $;选择优惠卡时y与x的函数关系式为$ y=0.75x+15 $.
(2)由图象可知:当$ 0\leq x<20 $时,选择次卡合算;当$ x=20 $时,选择次卡或优惠卡均比月卡合算;当$ 20<x<32 $时,选择优惠卡合算;当$ x=32 $时,选择优惠卡或月卡均比次卡合算;当$ x>32 $时,选择月卡合算.
(1)次卡对应的函数关系式为$ y_{1}=1.5x(x\geq 0) $,将$ x=20 $代入$ y_{1}=1.5x $,可得$ y_{1}=30 $,所以点B的坐标为(20,30).设优惠卡对应的函数关系式为$ y_{2}=kx+b(x\geq 0) $,将A(0,15),B(20,30)代入$ y_{2}=kx+b $,得$ b=15 $,$ 20k+b=30 $,$ k=0.75 $,所以优惠卡对应的函数关系式为$ y_{2}=0.75x+15(x\geq 0) $.将D(32,m)代入$ y_{2}=0.75x+15 $,可得$ m=39 $,将C(n,39)代入$ y_{1}=1.5x $,可得$ n=26 $,所以$ m=39 $,$ n=26 $.选择次卡时y与x的函数关系式为$ y=1.5x $;选择优惠卡时y与x的函数关系式为$ y=0.75x+15 $.
(2)由图象可知:当$ 0\leq x<20 $时,选择次卡合算;当$ x=20 $时,选择次卡或优惠卡均比月卡合算;当$ 20<x<32 $时,选择优惠卡合算;当$ x=32 $时,选择优惠卡或月卡均比次卡合算;当$ x>32 $时,选择月卡合算.
查看更多完整答案,请扫码查看


