第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
7. 【阅读理解】
如何判断无理数的大小范围呢? 我们可以这样做:
因为$25<30<36$,
所以$\sqrt{25}<\sqrt{30}<\sqrt{36}$,
即$5<\sqrt{30}<6$,
因此$\sqrt{30}$是介于5与6之间的一个数.
由此我们可以得到这样的结论:$\sqrt{30}$的整数部分是5,小数部分是$\sqrt{30}-5$.
【问题解决】
(1) 下列无理数在3与4之间的是(
A. $\sqrt{7}$
B. $2\sqrt{2}$
C. $\sqrt{13}$
D. $\sqrt{17}$
(2) $\sqrt{11}$的整数部分是
(3) $\sqrt{21}-2的整数部分为a$,小数部分为$b$,则$b-a= $
如何判断无理数的大小范围呢? 我们可以这样做:
因为$25<30<36$,
所以$\sqrt{25}<\sqrt{30}<\sqrt{36}$,
即$5<\sqrt{30}<6$,
因此$\sqrt{30}$是介于5与6之间的一个数.
由此我们可以得到这样的结论:$\sqrt{30}$的整数部分是5,小数部分是$\sqrt{30}-5$.
【问题解决】
(1) 下列无理数在3与4之间的是(
C
).A. $\sqrt{7}$
B. $2\sqrt{2}$
C. $\sqrt{13}$
D. $\sqrt{17}$
(2) $\sqrt{11}$的整数部分是
3
,小数部分是$\sqrt{11}-3$
.(3) $\sqrt{21}-2的整数部分为a$,小数部分为$b$,则$b-a= $
$\sqrt{21}-6$
.
答案:
1. (1)
对于选项A:
因为$4\lt7\lt9$,根据$\sqrt{4}\lt\sqrt{7}\lt\sqrt{9}$,即$2\lt\sqrt{7}\lt3$。
对于选项B:
先计算$2\sqrt{2}=\sqrt{8}$,因为$4\lt8\lt9$,所以$\sqrt{4}\lt\sqrt{8}\lt\sqrt{9}$,即$2\lt2\sqrt{2}\lt3$。
对于选项C:
因为$9\lt13\lt16$,所以$\sqrt{9}\lt\sqrt{13}\lt\sqrt{16}$,即$3\lt\sqrt{13}\lt4$。
对于选项D:
因为$16\lt17\lt25$,所以$\sqrt{16}\lt\sqrt{17}\lt\sqrt{25}$,即$4\lt\sqrt{17}\lt5$。
所以在$3$与$4$之间的无理数是$\sqrt{13}$,答案是C。
2. (2)
因为$9\lt11\lt16$,根据$\sqrt{9}\lt\sqrt{11}\lt\sqrt{16}$,即$3\lt\sqrt{11}\lt4$。
所以$\sqrt{11}$的整数部分是$3$,小数部分是$\sqrt{11}-3$。
3. (3)
因为$16\lt21\lt25$,所以$\sqrt{16}\lt\sqrt{21}\lt\sqrt{25}$,即$4\lt\sqrt{21}\lt5$。
那么$4 - 2\lt\sqrt{21}-2\lt5 - 2$,也就是$2\lt\sqrt{21}-2\lt3$。
所以$\sqrt{21}-2$的整数部分$a = 2$,小数部分$b=\sqrt{21}-2 - 2=\sqrt{21}-4$。
则$b - a=\sqrt{21}-4-2=\sqrt{21}-6$。
综上,答案依次为:(1)C;(2)$3$,$\sqrt{11}-3$;(3)$\sqrt{21}-6$。
对于选项A:
因为$4\lt7\lt9$,根据$\sqrt{4}\lt\sqrt{7}\lt\sqrt{9}$,即$2\lt\sqrt{7}\lt3$。
对于选项B:
先计算$2\sqrt{2}=\sqrt{8}$,因为$4\lt8\lt9$,所以$\sqrt{4}\lt\sqrt{8}\lt\sqrt{9}$,即$2\lt2\sqrt{2}\lt3$。
对于选项C:
因为$9\lt13\lt16$,所以$\sqrt{9}\lt\sqrt{13}\lt\sqrt{16}$,即$3\lt\sqrt{13}\lt4$。
对于选项D:
因为$16\lt17\lt25$,所以$\sqrt{16}\lt\sqrt{17}\lt\sqrt{25}$,即$4\lt\sqrt{17}\lt5$。
所以在$3$与$4$之间的无理数是$\sqrt{13}$,答案是C。
2. (2)
因为$9\lt11\lt16$,根据$\sqrt{9}\lt\sqrt{11}\lt\sqrt{16}$,即$3\lt\sqrt{11}\lt4$。
所以$\sqrt{11}$的整数部分是$3$,小数部分是$\sqrt{11}-3$。
3. (3)
因为$16\lt21\lt25$,所以$\sqrt{16}\lt\sqrt{21}\lt\sqrt{25}$,即$4\lt\sqrt{21}\lt5$。
那么$4 - 2\lt\sqrt{21}-2\lt5 - 2$,也就是$2\lt\sqrt{21}-2\lt3$。
所以$\sqrt{21}-2$的整数部分$a = 2$,小数部分$b=\sqrt{21}-2 - 2=\sqrt{21}-4$。
则$b - a=\sqrt{21}-4-2=\sqrt{21}-6$。
综上,答案依次为:(1)C;(2)$3$,$\sqrt{11}-3$;(3)$\sqrt{21}-6$。
1. 物理学家焦耳发现电流通过导体时可以产生热量. 电流发热的功率公式为$P= I^{2}R$,其中$P(W)$为电功率,$I(A)$为电流强度,$R(\Omega)$为电阻. 已知某电热炉的发热功率为1800 W,电阻为40 Ω,则这个电热炉的电流$I$介于(
A.5 A和6 A之间
B.6 A和7 A之间
C.7 A和8 A之间
D.8 A和9 A之间
B
).A.5 A和6 A之间
B.6 A和7 A之间
C.7 A和8 A之间
D.8 A和9 A之间
答案:
B
2. 已知$a= \sqrt{2023}-\sqrt{2022}$,$b= \sqrt{2024}-\sqrt{2023}$,$c= \sqrt{2025}-\sqrt{2024}$,下列结论正确的是(
A.$a>b>c$
B.$c>b>a$
C.$b>a>c$
D.$b>c>a$
A
).A.$a>b>c$
B.$c>b>a$
C.$b>a>c$
D.$b>c>a$
答案:
A
3. 满足$m>|\sqrt{10}-1|的整数m$的值可能是(
A.3
B.2
C.1
D.0
A
).A.3
B.2
C.1
D.0
答案:
A
4. 如图①,在$\triangle ABC$中,$AB= BC= 2$,$\angle B= 120^{\circ}$,$M是BC$的中点. 设$AM= a$,则表示数$a$的点落在图②数轴上所标4段中的(
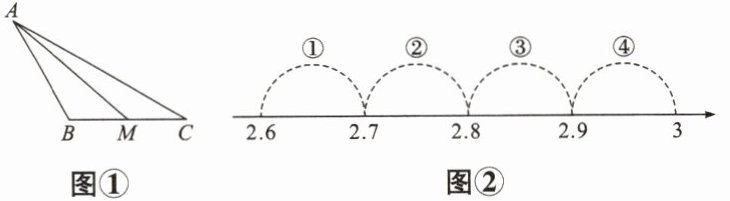
A.①段
B.②段
C.③段
D.④段
A
).
A.①段
B.②段
C.③段
D.④段
答案:
A
5. 一个正三角形的边长为6 cm,高为$h$,则$h= $
$3\sqrt{3}$
cm,若将$h$精确到个位,则$h$约为5.2
cm(结果精确到0.1 cm).
答案:
$3\sqrt3 5.2$
6. 已知$44^{2}= 1936$,$45^{2}= 2025$,$46^{2}= 2116$,$47^{2}= 2209$,若$n$为整数,且$n<\sqrt{2170}<n+1$,则$n$的值为
46
.
答案:
46
7. 比较大小:$\frac{\sqrt{5}+1}{2}$
>
$\frac{8}{5}$(填“>”“<”或“=”).
答案:
>
8. 在课堂上,老师出了一道题:比较$\frac{\sqrt{19}-2}{3}与\frac{2}{3}$的大小. 小明的解法如下:
解:$\frac{\sqrt{19}-2}{3}-\frac{2}{3}= \frac{\sqrt{19}-2-2}{3}= \frac{\sqrt{19}-4}{3}$,
$\because4^{2}= 16<19$,$\therefore\sqrt{19}>4$,$\therefore\sqrt{19}-4>0$,
$\therefore\frac{\sqrt{19}-4}{3}>0$,$\therefore\frac{\sqrt{19}-2}{3}>\frac{2}{3}$.
我们把这种比较大小的方法称为“作差法”.
(1) 根据上述材料填空(在横线上填“>”“=”或“<”).
① 若$a-b>0$,则$a$
② 若$a-b= 0$,则$a$
③ 若$a-b<0$,则$a$
(2) 利用上述方法比较$\frac{\sqrt{19}-3}{2}与\frac{3}{2}$的大小.
解:$\frac{\sqrt{19}-2}{3}-\frac{2}{3}= \frac{\sqrt{19}-2-2}{3}= \frac{\sqrt{19}-4}{3}$,
$\because4^{2}= 16<19$,$\therefore\sqrt{19}>4$,$\therefore\sqrt{19}-4>0$,
$\therefore\frac{\sqrt{19}-4}{3}>0$,$\therefore\frac{\sqrt{19}-2}{3}>\frac{2}{3}$.
我们把这种比较大小的方法称为“作差法”.
(1) 根据上述材料填空(在横线上填“>”“=”或“<”).
① 若$a-b>0$,则$a$
>
$b$;② 若$a-b= 0$,则$a$
=
$b$;③ 若$a-b<0$,则$a$
<
$b$.(2) 利用上述方法比较$\frac{\sqrt{19}-3}{2}与\frac{3}{2}$的大小.
答案:
$(1)$ 填空
① 若$a - b>0$,根据不等式的基本性质,移项可得$a>b$;
② 若$a - b = 0$,移项可得$a=b$;
③ 若$a - b<0$,移项可得$a<b$。
故答案依次为:$>$;$=$;$<$。
$(2)$ 比较$\frac{\sqrt{19}-3}{2}$与$\frac{3}{2}$的大小
解:利用作差法,计算$\frac{\sqrt{19}-3}{2}-\frac{3}{2}$。
根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$\frac{\sqrt{19}-3}{2}-\frac{3}{2}=\frac{\sqrt{19}-3 - 3}{2}=\frac{\sqrt{19}-6}{2}$。
因为$6^{2}=36$,而$19<36$,根据算术平方根的性质,若$m>n>0$,则$\sqrt{m}>\sqrt{n}$,所以$\sqrt{19}<6$。
那么$\sqrt{19}-6<0$,进而$\frac{\sqrt{19}-6}{2}<0$。
因为$\frac{\sqrt{19}-3}{2}-\frac{3}{2}<0$,根据$(1)$中作差法的结论,所以$\frac{\sqrt{19}-3}{2}<\frac{3}{2}$。
综上,答案依次为:$(1)$ $>$,$=$,$<$;$(2)$ $\boldsymbol{\frac{\sqrt{19}-3}{2}<\frac{3}{2}}$。
① 若$a - b>0$,根据不等式的基本性质,移项可得$a>b$;
② 若$a - b = 0$,移项可得$a=b$;
③ 若$a - b<0$,移项可得$a<b$。
故答案依次为:$>$;$=$;$<$。
$(2)$ 比较$\frac{\sqrt{19}-3}{2}$与$\frac{3}{2}$的大小
解:利用作差法,计算$\frac{\sqrt{19}-3}{2}-\frac{3}{2}$。
根据同分母分数减法法则$\frac{a}{c}-\frac{b}{c}=\frac{a - b}{c}$($c\neq0$),则$\frac{\sqrt{19}-3}{2}-\frac{3}{2}=\frac{\sqrt{19}-3 - 3}{2}=\frac{\sqrt{19}-6}{2}$。
因为$6^{2}=36$,而$19<36$,根据算术平方根的性质,若$m>n>0$,则$\sqrt{m}>\sqrt{n}$,所以$\sqrt{19}<6$。
那么$\sqrt{19}-6<0$,进而$\frac{\sqrt{19}-6}{2}<0$。
因为$\frac{\sqrt{19}-3}{2}-\frac{3}{2}<0$,根据$(1)$中作差法的结论,所以$\frac{\sqrt{19}-3}{2}<\frac{3}{2}$。
综上,答案依次为:$(1)$ $>$,$=$,$<$;$(2)$ $\boldsymbol{\frac{\sqrt{19}-3}{2}<\frac{3}{2}}$。
查看更多完整答案,请扫码查看


