《2025年新课堂学习与探究八年级数学上册北师大版》

3. 下列正方形的边长不是有理数的是(A)。
A.面积为 25 的正方形
B.面积为$\frac{4}{25}$的正方形
C.面积为 8 的正方形
D.面积为 1.44 的正方形

答案： A

4. 在实数$-(-3.14159),1.010010001…$(相邻两个 1 之间依次多 1 个 0),$-(-1)^{2026},-|-\frac{3}{4}|,4.\dot{2}\dot{1},\frac{π}{3},\frac{22}{7}$中,分数有4个。

答案： 4

5. 若面积为 15 的正方形的边长的整数部分为 a,面积为 56 的正方形的边长的整数部分为 b,则$a + b = $10。

答案： 10

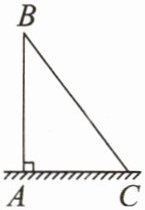
6. 如图,现要从离地面 5 m 的电线杆上的 B 处向地面 C 处拉一条钢丝绳来固定电线杆。若固定点 C 到点 A 的距离为 3 m,则钢丝绳 BC 的长度为5.8m(精确到十分位)。

答案： 5.8

7. 如图,在$5×5$的正方形网格中,每个小正方形的边长都为 1,请在给定网格中按下列要求画出图形。
(1)从点 A 出发画一条线段 AB,使它的另一个端点 B 在格点(即小正方形的顶点)上,且$AB^{2}= 8$。
(2)画出所有以(1)中的 AB 为边的等腰三角形,使另一个顶点在格点上,且另外两边的长度都是无理数。

答案：
解:
(1)线段AB如图所示.
(2)△ABD,△ABC如图所示.

1. 一个长方形的长与宽分别是 6 cm,3 cm,则它的对角线的长是(D)。
A.整数
B.分数
C.有理数
D.无限不循环小数

答案： D

2. 下列说法正确的是(B)。
A.有理数只是有限小数
B.无理数是无限不循环小数
C.无限小数都是无理数
D.$\frac{π}{3}$是分数

答案： B

3. 在数$-8,0.161616…,0.\dot{6},0.080080008…$(相邻两个 8 之间依次增加 1 个 0),$2.5,30,π$中,无理数有(C)。
A.0 个
B.1 个
C.2 个
D.3 个

答案： C

4. 如图,在$4×4$的正方形网格中,所有线段的端点都在格点上,则这些线段的长度是无理数的有(B)。

A.1 条
B.2 条
C.3 条
D.4 条

答案： B

5. 请写出满足条件$x - 3 ＜ 0$的一个无理数：$\sqrt{2}$(答案不唯一.)。

答案： $\sqrt{2}$(答案不唯一.)

6. 若两个连续的整数 a,b 满足$a^{2}＜13＜b^{2}$,则$\frac{1}{ab}$的值为$\frac{1}{12}$。

答案： $\frac{1}{12}$