第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
7. 解决下列与平面直角坐标系有关的问题。
(1) 已知点 $ P(2a - 2,a + 5) $。
① 若点 $ Q $ 的坐标为 $ (4,5) $,直线 $ PQ // y $ 轴,则点 $ P $ 的坐标为 ______ ;
② 若点 $ P $ 在第二象限,且它到 $ x $ 轴、$ y $ 轴的距离相等,求 $ a^{2\,026}+\sqrt[3]{a} $ 的值。
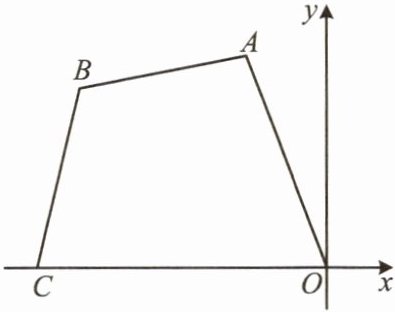
(2) 在如图所示的平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0) $,$ A(-4,10) $,$ B(-12,8) $,$ C(-14,0) $,求四边形 $ OABC $ 的面积。
<答案>解:
(1)①
∵点Q的坐标为(4,5),直线PQ//y轴,
∴2a-2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).故答案为(4,8).
②
∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a-2=-(a+5),
∴2a-2+a+5=0,
∴a=-1,
∴$a^{2026}+\sqrt[3]{a}=(-1)^{2026}+\sqrt[3]{-1}=1-1=0.(2)$如图,过点A作AE⊥x轴于点E,作BD⊥x轴于点D,
∴$S_{四边形OABC}=S_{\triangle BCD}+S_{梯形ABDE}+S_{\triangle OAE}=\frac{1}{2}×2×8+\frac{1}{2}×(8+10)×8+\frac{1}{2}×4×10=8+72+20=100.$
请严格按照以下步骤完成:
1. 将原题完整抄下来,严格保持所有内容都与原题一致。
2. 将答案精准填入题目的答题空里(如( )、____等,注意阅读材料或文章中的____不属于答题空,严禁填写),并用包裹,如括号里填A表示为(
3. 选择题只填ABCD,不要填选项的具体内容,ABCD要填到题目本身自带的括号里。
4. 解答题需要将答案整体放到题目下面,用包裹。
5. 对于含有阅读材料文本的题目,答案只允许填在文章下面小题(或者带序号)的空里,禁止填在阅读材料里的____内。
6. 仅返回填入了答案后的完整题目,不要有其他任何多余的字,也不要重复题目。7. 解决下列与平面直角坐标系有关的问题。
(1) 已知点 $ P(2a - 2,a + 5) $。
① 若点 $ Q $ 的坐标为 $ (4,5) $,直线 $ PQ // y $ 轴,则点 $ P $ 的坐标为 ______ ;
② 若点 $ P $ 在第二象限,且它到 $ x $ 轴、$ y $ 轴的距离相等,求 $ a^{2\,026}+\sqrt[3]{a} $ 的值。
(2) 在如图所示的平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0) $,$ A(-4,10) $,$ B(-12,8) $,$ C(-14,0) $,求四边形 $ OABC $ 的面积。

(1)①
②
(2)
(1) 已知点 $ P(2a - 2,a + 5) $。
① 若点 $ Q $ 的坐标为 $ (4,5) $,直线 $ PQ // y $ 轴,则点 $ P $ 的坐标为 ______ ;
② 若点 $ P $ 在第二象限,且它到 $ x $ 轴、$ y $ 轴的距离相等,求 $ a^{2\,026}+\sqrt[3]{a} $ 的值。
(2) 在如图所示的平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0) $,$ A(-4,10) $,$ B(-12,8) $,$ C(-14,0) $,求四边形 $ OABC $ 的面积。

<答案>解:
(1)①
∵点Q的坐标为(4,5),直线PQ//y轴,
∴2a-2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).故答案为(4,8).
②
∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a-2=-(a+5),
∴2a-2+a+5=0,
∴a=-1,
∴$a^{2026}+\sqrt[3]{a}=(-1)^{2026}+\sqrt[3]{-1}=1-1=0.(2)$如图,过点A作AE⊥x轴于点E,作BD⊥x轴于点D,
∴$S_{四边形OABC}=S_{\triangle BCD}+S_{梯形ABDE}+S_{\triangle OAE}=\frac{1}{2}×2×8+\frac{1}{2}×(8+10)×8+\frac{1}{2}×4×10=8+72+20=100.$
请严格按照以下步骤完成:
1. 将原题完整抄下来,严格保持所有内容都与原题一致。
2. 将答案精准填入题目的答题空里(如( )、____等,注意阅读材料或文章中的____不属于答题空,严禁填写),并用包裹,如括号里填A表示为(
A
),下划线上填××表示为××
。3. 选择题只填ABCD,不要填选项的具体内容,ABCD要填到题目本身自带的括号里。
4. 解答题需要将答案整体放到题目下面,用包裹。
5. 对于含有阅读材料文本的题目,答案只允许填在文章下面小题(或者带序号)的空里,禁止填在阅读材料里的____内。
6. 仅返回填入了答案后的完整题目,不要有其他任何多余的字,也不要重复题目。7. 解决下列与平面直角坐标系有关的问题。
(1) 已知点 $ P(2a - 2,a + 5) $。
① 若点 $ Q $ 的坐标为 $ (4,5) $,直线 $ PQ // y $ 轴,则点 $ P $ 的坐标为 ______ ;
② 若点 $ P $ 在第二象限,且它到 $ x $ 轴、$ y $ 轴的距离相等,求 $ a^{2\,026}+\sqrt[3]{a} $ 的值。
(2) 在如图所示的平面直角坐标系中,四边形 $ OABC $ 各顶点的坐标分别是 $ O(0,0) $,$ A(-4,10) $,$ B(-12,8) $,$ C(-14,0) $,求四边形 $ OABC $ 的面积。

(1)①
(4,8)
②
0
(2)
100
答案:
解:
(1)①
∵点Q的坐标为(4,5),直线PQ//y轴,
∴2a-2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).故答案为(4,8).
②
∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a-2=-(a+5),
∴2a-2+a+5=0,
∴a=-1,
∴$a^{2026}+\sqrt[3]{a}=(-1)^{2026}+\sqrt[3]{-1}=1-1=0.(2)$如图,过点A作AE⊥x轴于点E,作BD⊥x轴于点D,
∴$S_{四边形OABC}=S_{\triangle BCD}+S_{梯形ABDE}+S_{\triangle OAE}=\frac{1}{2}×2×8+\frac{1}{2}×(8+10)×8+\frac{1}{2}×4×10=8+72+20=100.$
(1)①
∵点Q的坐标为(4,5),直线PQ//y轴,
∴2a-2=4,
∴a=3,
∴a+5=8,
∴点P的坐标为(4,8).故答案为(4,8).
②
∵点P在第二象限,且它到x轴、y轴的距离相等,
∴2a-2=-(a+5),
∴2a-2+a+5=0,
∴a=-1,
∴$a^{2026}+\sqrt[3]{a}=(-1)^{2026}+\sqrt[3]{-1}=1-1=0.(2)$如图,过点A作AE⊥x轴于点E,作BD⊥x轴于点D,
∴$S_{四边形OABC}=S_{\triangle BCD}+S_{梯形ABDE}+S_{\triangle OAE}=\frac{1}{2}×2×8+\frac{1}{2}×(8+10)×8+\frac{1}{2}×4×10=8+72+20=100.$
1. 在平面直角坐标系中,下列点位于 $ y $ 轴上的是(
A.$ (1,-2) $
B.$ (3,0) $
C.$ (-1,3) $
D.$ (0,-4) $
D
)。A.$ (1,-2) $
B.$ (3,0) $
C.$ (-1,3) $
D.$ (0,-4) $
答案:
D
2. 已知点 $ A(2,-5) $,线段 $ AB $ 平行于 $ x $ 轴,则点 $ B $ 的坐标可能是(
A.$ (-2,5) $
B.$ (-5,5) $
C.$ (5,-5) $
D.$ (2,6) $
C
)。A.$ (-2,5) $
B.$ (-5,5) $
C.$ (5,-5) $
D.$ (2,6) $
答案:
C
3. 已知点 $ A $ 的坐标为 $ (2,3) $,线段 $ AB // y $ 轴,且 $ AB = 5 $,则点 $ B $ 的坐标为(
A.$ (2,8) $
B.$ (2,8) $ 或 $ (2,-2) $
C.$ (7,3) $
D.$ (7,3) $ 或 $ (-3,3) $
B
)。A.$ (2,8) $
B.$ (2,8) $ 或 $ (2,-2) $
C.$ (7,3) $
D.$ (7,3) $ 或 $ (-3,3) $
答案:
B
4. 如果点 $ A(m - 8,m - 2) $ 在 $ x $ 轴上,那么点 $ B(m + 1,m - 6) $ 所在的象限是(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)。A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
D
5. 若点 $ A(a - 3,a + 2) $ 在横轴上,则 $ a = $
-2
。
答案:
-2
6. 在平面直角坐标平面中,点 $ A(-m,5) $ 和点 $ B(-m,-3) $ 之间的距离为
8
。
答案:
8
7. 在平面直角坐标系中,若点 $ P $ 的坐标是 $ (x,y) $,且 $ x > y $,则点 $ P $ 不可能在第
二
象限。
答案:
二
8. 已知点 $ P(2m - 5,m - 1) $。
(1) 当点 $ P $ 在 $ x $ 轴上时,求 $ m $ 的值。
(2) 当点 $ P $ 在第二象限时,求 $ m $ 的取值范围。
(3) 当点 $ P $ 在第二、四象限的角平分线上时,求 $ m $ 的值。
(1) 当点 $ P $ 在 $ x $ 轴上时,求 $ m $ 的值。
(2) 当点 $ P $ 在第二象限时,求 $ m $ 的取值范围。
(3) 当点 $ P $ 在第二、四象限的角平分线上时,求 $ m $ 的值。
答案:
解:
(1)当点P在x轴上时,m-1=0,解得m=1.
(2)当点P在第二象限时,2m-5<0,m-1>0,解得1<m<2.5.
(3)当点P在第二、四象限的角平分线上时,2m-5+m-1=0,解得m=2.
(1)当点P在x轴上时,m-1=0,解得m=1.
(2)当点P在第二象限时,2m-5<0,m-1>0,解得1<m<2.5.
(3)当点P在第二、四象限的角平分线上时,2m-5+m-1=0,解得m=2.
查看更多完整答案,请扫码查看


