第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
1. 利用勾股定理解决折叠问题
(1) 全等关系:折叠前后图形
(2) 折痕的作用:折痕是
(3) 直角三角形的生成:折叠常构造新直角三角形,便于用
(1) 全等关系:折叠前后图形
全等
,对应边、对应角相等
。(2) 折痕的作用:折痕是
对称轴
,可能隐含角平分线或垂直平分线。(3) 直角三角形的生成:折叠常构造新直角三角形,便于用
勾股定理
列方程。
答案:
(1)全等,相等;
(2)对称轴;
(3)勾股定理
(1)全等,相等;
(2)对称轴;
(3)勾股定理
2. 圆柱(或圆锥)侧面上两点间的最短距离
把圆柱(或圆锥)侧面展开成
把圆柱(或圆锥)侧面展开成
平面
图形,依据“两点之间,线段
最短”,以最短路线为斜边构造直角
三角形,利用勾股
定理求解。
答案:
平面,线段,直角,勾股
平面,线段,直角,勾股
3. 长方体(或正方体)侧面上两点间的最短距离
若计算同一个面上的两点之间的距离,比较容易。若计算不同面上的两点之间的距离,就必须把它们转化到同一个
若计算同一个面上的两点之间的距离,比较容易。若计算不同面上的两点之间的距离,就必须把它们转化到同一个
平面
内,即把长方体(或正方体)设法展开成平面图形
,使计算距离的两个点处在同一个平面
中,这样就可以利用勾股
定理来解决。
答案:
平面,平面图形,平面,勾股
平面,平面图形,平面,勾股
1. 如图,在长方形 $ABCD$ 中,$AB = 6$,$BC = 8$,将 $\triangle ABD$ 沿 $BD$ 折叠,使点 $A$ 落在点 $P$ 处,$PD$ 交 $CB$ 于点 $Q$,求 $CQ$ 的长。

[知识点2] 圆柱(或圆锥)侧面上两点间的最短距离

[知识点2] 圆柱(或圆锥)侧面上两点间的最短距离
答案:
1. 解:在长方形 ABCD 中,
∠A=∠C=90°,AB=CD=6,
由折叠的性质可知∠A=∠P=90°,BP=AB,
∴∠P=∠C,BP=CD.
在△BPQ 和△DCQ 中,
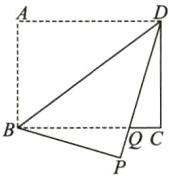
∵{∠BQP=∠DQC,
∠P=∠C,
BP=DC,
∴△BPQ≌△DCQ(AAS),
∴BQ=DQ.
设 CQ=x,则 DQ=BQ=BC - CQ=8 - x.
在Rt△CDQ 中,由勾股定理得CQ²+CD²=DQ²,
即x²+6²=(8 - x)²,解得x=7/4,
∴CQ 的长为7/4.
1. 解:在长方形 ABCD 中,
∠A=∠C=90°,AB=CD=6,
由折叠的性质可知∠A=∠P=90°,BP=AB,
∴∠P=∠C,BP=CD.
在△BPQ 和△DCQ 中,

∵{∠BQP=∠DQC,
∠P=∠C,
BP=DC,
∴△BPQ≌△DCQ(AAS),
∴BQ=DQ.
设 CQ=x,则 DQ=BQ=BC - CQ=8 - x.
在Rt△CDQ 中,由勾股定理得CQ²+CD²=DQ²,
即x²+6²=(8 - x)²,解得x=7/4,
∴CQ 的长为7/4.
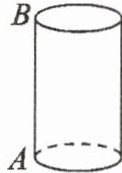
2. 如图,一只蚂蚁在底面半径为 $20\mathrm{cm}$、高为 $30\pi\mathrm{cm}$ 的圆柱下底面的点 $A$ 处,发现自己正上方圆柱上底面的点 $B$ 处有一只小昆虫,便决定捕捉这只小昆虫。为了不引起这只小昆虫的注意,它故意不走直线,绕着圆柱沿曲线爬行,从背后对小昆虫进行突然袭击,结果袭击成功,得到了一顿美餐。蚂蚁至少爬行多远才能捕捉到小昆虫?
[知识点3] 长方体(或正方体)侧面上两点间的最短距离

[知识点3] 长方体(或正方体)侧面上两点间的最短距离
答案:
2. 解:如图,将圆柱体的侧面沿 AB 剪开铺平,则对角线 AB 即为蚂蚁爬行的最短路线.
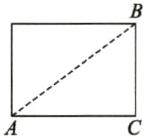
在Rt△ACB 中,AC=40πcm,BC=30πcm,
则AB²=AC²+BC²=(40π)²+(30π)²=(50π)²,
解得AB=50π.
答:蚂蚁至少爬行50πcm 才能捕捉到小昆虫.
2. 解:如图,将圆柱体的侧面沿 AB 剪开铺平,则对角线 AB 即为蚂蚁爬行的最短路线.

在Rt△ACB 中,AC=40πcm,BC=30πcm,
则AB²=AC²+BC²=(40π)²+(30π)²=(50π)²,
解得AB=50π.
答:蚂蚁至少爬行50πcm 才能捕捉到小昆虫.
查看更多完整答案,请扫码查看


