《2025年新课堂学习与探究八年级数学上册北师大版》

8. (扬州中考)清代扬州数学家罗士琳痴迷于勾股定理的研究,提出了推算勾股数的“罗士琳法则”。法则的提出,不仅简化了勾股数的生成过程,也体现了中国传统数学在数论领域的贡献。由此法则写出了下列几组勾股数：
①$3$,$4$,$5$；
②$5$,$12$,$13$；
③$7$,$24$,$25$；
④$9$,$40$,$41$；
……
根据上述规律,第⑤组勾股数为11,60,61。

答案： 11,60,61

9. (南通中考)勾股数是指能成为直角三角形的3条边长的3个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》。现有勾股数$a$,$b$,$c$,其中$a$,$b均小于c$,$a = \frac{1}{2}m^{2} - \frac{1}{2}$,$c = \frac{1}{2}m^{2} + \frac{1}{2}$,$m$是大于1的奇数,则$b = $m(用含$m$的式子表示)。

答案： m

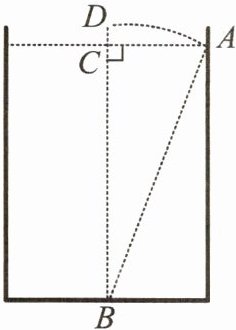
10. (巴中中考)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐。问：水深几何？”这是我国数学史上的“葭生池中”问题,示意图如图所示,$AC = 5$,$DC = 1$,$BD = BA$,则$BC = $(C)。

A.$8$
B.$10$
C.$12$
D.$13$

答案： C

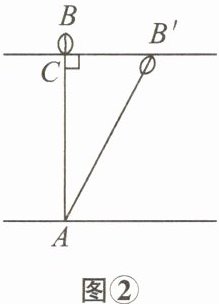
11. (吉林中考)图①中有一首诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,示意图如图②,其中$AB = AB'$,$AB \perp B'C于点C$,$BC = 0.5$尺,$B'C = 2$尺。设$AC的长度为x$尺,则可列方程$x^{2}+2^{2}=(x+0.5)^{2}$。

答案： $x^{2}+2^{2}=(x+0.5)^{2}$

12. (东营中考)一艘船由$A港沿北偏东60^{\circ}方向航行30$km至$B$港,然后沿北偏西$30^{\circ}方向航行40$km至$C$港,则$A$,$C$两港之间的距离为50km。

答案： 50

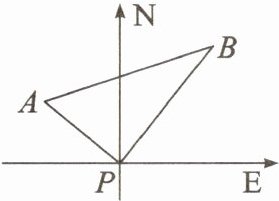
13. (玉林中考)如图,某港口$P$位于东西方向的海岸线上,甲、乙轮船同时离开港口$P$,各自沿一固定方向航行。甲、乙轮船每小时分别航行$12海里和16$海里,$1小时后两船分别位于点A$,$B$处,且相距$20$海里。如果知道甲船沿北偏西$40^{\circ}$方向航行,那么乙船沿北偏东$50^{\circ }$方向航行。

答案： 北偏东$50^{\circ }$