《2025年新课堂学习与探究八年级数学上册北师大版》

9. 计算下列题.
(1)$(\sqrt{15} + 5)(\sqrt{15} - 5)$
(2)$(3\sqrt{2} - \sqrt{3})^2$
(3)$(\sqrt{8} - \sqrt{\frac{1}{2}})×\sqrt{2}$
(4)$\frac{\sqrt{45} - \sqrt{20}}{\sqrt{5}}$

答案： 1. （1）
解：根据平方差公式$(a + b)(a - b)=a^{2}-b^{2}$，这里$a = \sqrt{15}$，$b = 5$。
则$(\sqrt{15}+5)(\sqrt{15}-5)=(\sqrt{15})^{2}-5^{2}$
因为$(\sqrt{15})^{2}=15$，$5^{2}=25$，所以$(\sqrt{15})^{2}-5^{2}=15 - 25=-10$。
2. （2）
解：根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$，这里$a = 3\sqrt{2}$，$b=\sqrt{3}$。
则$(3\sqrt{2}-\sqrt{3})^{2}=(3\sqrt{2})^{2}-2×3\sqrt{2}×\sqrt{3}+(\sqrt{3})^{2}$
因为$(3\sqrt{2})^{2}=9×2 = 18$，$2×3\sqrt{2}×\sqrt{3}=6\sqrt{6}$，$(\sqrt{3})^{2}=3$。
所以$(3\sqrt{2}-\sqrt{3})^{2}=18-6\sqrt{6}+3=21 - 6\sqrt{6}$。
3. （3）
解：根据乘法分配律$(a - b)c=ac - bc$，这里$a=\sqrt{8}$，$b = \sqrt{\frac{1}{2}}$，$c=\sqrt{2}$。
则$(\sqrt{8}-\sqrt{\frac{1}{2}})×\sqrt{2}=\sqrt{8}×\sqrt{2}-\sqrt{\frac{1}{2}}×\sqrt{2}$
因为$\sqrt{8}×\sqrt{2}=\sqrt{16}=4$，$\sqrt{\frac{1}{2}}×\sqrt{2}=\sqrt{1}=1$。
所以$(\sqrt{8}-\sqrt{\frac{1}{2}})×\sqrt{2}=4 - 1=3$。
4. （4）
解：先将分子中的二次根式化简，$\sqrt{45}=\sqrt{9×5}=3\sqrt{5}$，$\sqrt{20}=\sqrt{4×5}=2\sqrt{5}$。
则$\frac{\sqrt{45}-\sqrt{20}}{\sqrt{5}}=\frac{3\sqrt{5}-2\sqrt{5}}{\sqrt{5}}$。
分子$3\sqrt{5}-2\sqrt{5}=(3 - 2)\sqrt{5}=\sqrt{5}$。
所以$\frac{\sqrt{45}-\sqrt{20}}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1$。
综上，答案依次为：（1）$-10$；（2）$21 - 6\sqrt{6}$；（3）$3$；（4）$1$。

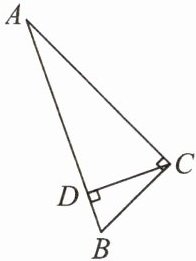
10. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ},AB = \sqrt{10},BC = \sqrt{2}$. 求斜边$AB上的高CD$.

答案： 1. 首先，根据勾股定理求$AC$的长度：
在$Rt\triangle ABC$中，由勾股定理$a^{2}+b^{2}=c^{2}$（其中$c$为斜边，$a$、$b$为两直角边），已知$AB = c=\sqrt{10}$，$BC = a=\sqrt{2}$，设$AC = b$，则$AC=\sqrt{AB^{2}-BC^{2}}$。
代入数值可得$AC=\sqrt{(\sqrt{10})^{2}-(\sqrt{2})^{2}}=\sqrt{10 - 2}=\sqrt{8}=2\sqrt{2}$。
2. 然后，根据三角形面积公式求$CD$：
三角形面积公式$S=\frac{1}{2}ab$（$a$、$b$为两直角边），对于$Rt\triangle ABC$，$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC$；同时$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD$（$CD$为$AB$边上的高）。
因为$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，所以$CD=\frac{AC\cdot BC}{AB}$。
把$AC = 2\sqrt{2}$，$BC=\sqrt{2}$，$AB=\sqrt{10}$代入$CD=\frac{AC\cdot BC}{AB}$中，可得$CD=\frac{2\sqrt{2}×\sqrt{2}}{\sqrt{10}}$。
计算$2\sqrt{2}×\sqrt{2}=2×2 = 4$，则$CD=\frac{4}{\sqrt{10}}=\frac{4\sqrt{10}}{10}=\frac{2\sqrt{10}}{5}$。
所以，斜边$AB$上的高$CD$为$\frac{2\sqrt{10}}{5}$。

11. 阅读下列材料,然后回答问题.
在进行二次根式运算时,我们有时会碰上形如$\frac{3}{\sqrt{5}},\sqrt{\frac{2}{3}},\frac{2}{\sqrt{3} + 1}$的式子,可以将它们进一步化简：
$\frac{3}{\sqrt{5}} = \frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}} = \frac{3}{5}\sqrt{5}$；Ⅰ
$\sqrt{\frac{2}{3}} = \sqrt{\frac{2×3}{3×3}} = \frac{\sqrt{6}}{3}$；Ⅱ
$\frac{2}{\sqrt{3} + 1} = \frac{2(\sqrt{3} - 1)}{(\sqrt{3} + 1)(\sqrt{3} - 1)} = \frac{2(\sqrt{3} - 1)}{(\sqrt{3})^2 - 1^2} = \sqrt{3} - 1$.Ⅲ
以上这种化简的方法叫作分母有理化.
$\frac{2}{\sqrt{3} + 1}$还可以用以下方法化简：
$\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{(\sqrt{3})^2 - 1^2}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1)(\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$.Ⅳ
(1)请用不同的方法化简$\frac{2}{\sqrt{5} + \sqrt{3}}$.
①参照Ⅲ式得$\frac{2}{\sqrt{5} + \sqrt{3}}= $$\sqrt{5}-\sqrt{3}$.
②参照Ⅳ式得$\frac{2}{\sqrt{5} + \sqrt{3}}= $$\sqrt{5}-\sqrt{3}$.
(2)化简：$\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + … + \frac{1}{\sqrt{2n + 1} + \sqrt{2n - 1}}$.
$\frac{\sqrt{2n + 1}-1}{2}$

答案： $(1)$
- ①参照Ⅲ式：
解：
$\begin{aligned}\frac{2}{\sqrt{5}+\sqrt{3}}&=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}\\&=\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^2 - (\sqrt{3})^2}\\&=\frac{2(\sqrt{5}-\sqrt{3})}{5 - 3}\\&=\sqrt{5}-\sqrt{3}\end{aligned}$
- ②参照Ⅳ式：
解：
$\begin{aligned}\frac{2}{\sqrt{5}+\sqrt{3}}&=\frac{5 - 3}{\sqrt{5}+\sqrt{3}}\\&=\frac{(\sqrt{5})^2 - (\sqrt{3})^2}{\sqrt{5}+\sqrt{3}}\\&=\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}\\&=\sqrt{5}-\sqrt{3}\end{aligned}$
$(2)$化简$\frac{1}{\sqrt{3}+1}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{7}+\sqrt{5}}+\cdots+\frac{1}{\sqrt{2n + 1}+\sqrt{2n - 1}}$
解：
先对每一项进行分母有理化：
$\frac{1}{\sqrt{3}+1}=\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}=\frac{\sqrt{3}-1}{2}$
$\frac{1}{\sqrt{5}+\sqrt{3}}=\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\frac{\sqrt{5}-\sqrt{3}}{2}$
$\frac{1}{\sqrt{7}+\sqrt{5}}=\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})}=\frac{\sqrt{7}-\sqrt{5}}{2}$
$\cdots$
$\frac{1}{\sqrt{2n + 1}+\sqrt{2n - 1}}=\frac{\sqrt{2n + 1}-\sqrt{2n - 1}}{(\sqrt{2n + 1}+\sqrt{2n - 1})(\sqrt{2n + 1}-\sqrt{2n - 1})}=\frac{\sqrt{2n + 1}-\sqrt{2n - 1}}{2}$
则原式$=\frac{\sqrt{3}-1}{2}+\frac{\sqrt{5}-\sqrt{3}}{2}+\frac{\sqrt{7}-\sqrt{5}}{2}+\cdots+\frac{\sqrt{2n + 1}-\sqrt{2n - 1}}{2}$
$=\frac{1}{2}[(\sqrt{3}-1)+(\sqrt{5}-\sqrt{3})+(\sqrt{7}-\sqrt{5})+\cdots+(\sqrt{2n + 1}-\sqrt{2n - 1})]$
去括号后可以发现中间项都可消去：
$=\frac{1}{2}(\sqrt{2n + 1}-1)$
综上，答案依次为：$(1)$①$\boldsymbol{\sqrt{5}-\sqrt{3}}$；②$\boldsymbol{\sqrt{5}-\sqrt{3}}$；$(2)$$\boldsymbol{\frac{\sqrt{2n + 1}-1}{2}}$。