《2025年新课堂学习与探究八年级数学上册北师大版》

5. 在式子①$y = 0.5x - 2$,②$y = |2x|$,③$3y + 5 = x$,④$y^{2} = 2x + 8$中,$y是x$的函数的是①②③(填序号)。

答案： ①②③

6. 已知函数$y = \begin{cases}2x^{2} + 4(x \leq 3) \\ 3x(x ＞ 3) \end{cases} $,当函数自变量$x = -1$时,$y = $6。

答案： 6

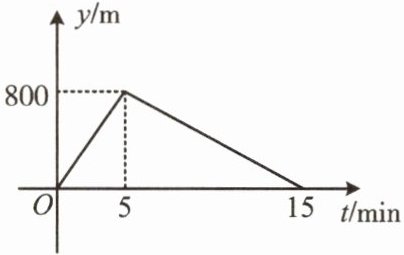
7. 小明从家跑步到学校,接着马上按原路步行回家。小明离家的路程$y(m)与时间t(min)$的函数图象如图所示,则小明回家的速度是每分钟步行80m。

答案： 80

8. 小李家的猕猴桃喜获丰收。在销售过程中,猕猴桃的销售额$y$(元)与销量$x$(千克)满足如下关系：

(1)在这个变化过程中,自变量是猕猴桃的销量,因变量是猕猴桃的销售额。
(2)猕猴桃的销售额$y$(元)与销售量$x$(千克)之间的关系式为$ y=6x $。
(3)当猕猴桃销售量为$100$千克时,销售额是多少元？
将$ x=100 $代入$ y=6x $,可得$ y=6×100=600 $(元).

答案：
(1)猕猴桃的销量 猕猴桃的销售额
(2)$ y=6x $
(3)将$ x=100 $代入$ y=6x $,可得$ y=6×100=600 $(元).

9. 快递员小李骑电动车去派送快递,行驶了一段时间后,想起要去附近的便利店取个包裹,于是又折回到刚经过的便利店,取到包裹后继续前往派送点,直到抵达派送点。他本次派送所用的时间与距出发地距离的关系示意图如图所示,根据图中提供的信息解答下列问题：
(1)图中自变量是时间,因变量是距出发地距离。
(2)出发地到派送点的路程是1500米,小李在便利店停留了4分钟。
(3)快递员小李出发后多长时间,距离派送点$600$米？
解:
(3)当$ 0≤t≤6 $时,速度为$ 1200÷6=200 $(米/分);当$ 6＜t≤8 $时,速度为$ (1200-600)÷(8-6)=300 $(米/分);当$ 8＜t≤12 $时,速度为0;当$ 12＜t≤14 $时,速度为$ (1500-600)÷(14-12)=450 $(米/分).设小李出发后t分钟,离派送点的距离是600米,当$ 0≤t≤6 $时,$ 200t=1500-600 $,得$ t=4.5 $;当$ 6＜t≤8 $时,$ 300(t-6)=600-(1500-1200) $,得$ t=7 $;当$ 12＜t≤14 $时,$ 1500-600-600=450(t-12) $,得$ t=12\frac{2}{3} $。
答:小李出发后4.5分钟或7分钟或$ 12\frac{2}{3} $分钟,离派送点的距离是600米。

答案： 解:
(1)时间 距出发地距离
(2)1500 4
(3)当$ 0≤t≤6 $时,速度为$ 1200÷6=200 $(米/分);当$ 6＜t≤8 $时,速度为$ (1200-600)÷(8-6)=300 $(米/分);当$ 8＜t≤12 $时,速度为0;当$ 12＜t≤14 $时,速度为$ (1500-600)÷(14-12)=450 $(米/分).设小李出发后t分钟,离派送点的距离是600米,当$ 0≤t≤6 $时,$ 200t=1500-600 $,得$ t=4.5 $;当$ 6＜t≤8 $时,$ 300(t-6)=600-(1500-1200) $,得$ t=7 $;当$ 12＜t≤14 $时,$ 1500-600-600=450(t-12) $,得$ t=12\frac{2}{3} $.
答:小李出发后4.5分钟或7分钟或$ 12\frac{2}{3} $分钟,离派送点的距离是600米.