《2025年新课堂学习与探究八年级数学上册北师大版》

3. 如果方程组$\begin{cases}3x + 2y = 6\\3x - 2y = 2\end{cases} 的解也是方程4x + y + 2a = 0$的解,那么$a$的值是-19/6。

答案： -19/6

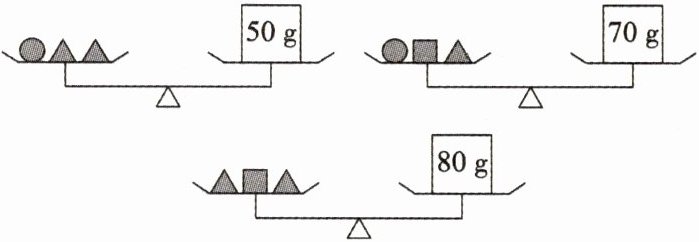
4. 设“●”“■”“▲”表示 3 种不同的物体,现用天平称了 3 次,每次都平衡,如图所示,那么这 3 种物体的质量分别为10 g,40 g,20 g。

答案： 10 g,40 g,20 g

5. 解下列三元一次方程组。
(1)$\begin{cases}x + y = 7\\2y + z = 6\\x - z = 7\end{cases} $ (2)$\begin{cases}2x + 2y + z = 4\\2x + y + 2z = 7\\x + 2y + 2z = -6\end{cases} $

答案： 5.解:
(1){x+y=7①,2y+z=6②,x-z=7③,②+③得x+2y=13④,④-①得y=6,把y=6代入④得x=1,把x=1代入③得z=-6,则方程组的解为{x=1,y=6,z=-6.
(2){2x+2y+z=4①,2x+y+2z=7②,x+2y+2z=-6③,②-③得x-y=13④,①×2-②得2x+3y=1⑤,④×3+⑤得5x=40,解得x=8,把x=8代入④得y=-5,把x=8,y=-5代入①得z=-2,则方程组的解为{x=8,y=-5,z=-2.

6. 某服装厂专门安排 210 名工人进行手工衬衣的缝制,每件衬衣由 2 个衣袖、1 个衣身和 1 个衣领组成。如果每人每天能够缝制衣袖 10 个,或衣身 15 个,或衣领 12 个,那么安排多少名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配套？

答案： 解:设应该安排x名工人缝制衣袖,y名工人缝制衣身,z名工人缝制衣领,才能使每天缝制出的衣袖、衣身、衣领正好配套.依题意得{x+y+z=210,10x∶15y∶12z=2∶1∶1,解得{x=120,y=40,z=50.答:应该安排120名工人缝制衣袖,才能使每天缝制出的衣袖、衣身、衣领正好配套.

1. 下列方程组不是三元一次方程组的是(D)。
A.$\begin{cases}x = 5\\x + y = 7\\x + y + z = 6\end{cases} $
B.$\begin{cases}x + y + z = 2\\x - y + z = 0\\x - z = 4\end{cases} $
C.$\begin{cases}x + y = 3\\y + z = 5\\x + z = 4\end{cases} $
D.$\begin{cases}x + y + 3z = 5\\x - 3y = 4z\\xy + yz = 1\end{cases} $

答案： D

2. 三元一次方程组$\begin{cases}x + y = 3\\y + z = 5\\z + x = 4\end{cases} $的解为(B)。
A.$\begin{cases}x = 0\\y = 2\\z = 3\end{cases} $
B.$\begin{cases}x = 1\\y = 2\\z = 3\end{cases} $
C.$\begin{cases}x = 1\\y = 0\\z = 3\end{cases} $
D.$\begin{cases}x = 3\\y = 1\\z = 1\end{cases} $

答案： B

3. 现有甲、乙、丙 3 种货物,若购 3 件甲、7 件乙、1 件丙,共需 64 元；若购 4 件甲、10 件乙、1 件丙,共需 79 元。若购 1 件甲、3 件乙,共需(C)。
A.13 元
B.14 元
C.15 元
D.16 元

答案： C

4. 现有 3 堆硬币,每枚硬币的面值相同。小李从第 1 堆取出和第 2 堆一样多的硬币放入第 2 堆,又从第 2 堆取出和第 3 堆一样多的硬币放入第 3 堆,最后从第 3 堆取出和现在的第 1 堆一样多的硬币放入第 1 堆,这样每堆有 16 枚硬币。原来第 1 堆有硬币(A)。
A.22 枚
B.16 枚
C.14 枚
D.12 枚

答案： A