第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
1. 计算:$\sqrt{4}= (
A.±2
B.2
C.$\pm\sqrt{2}$
D.$\sqrt{2}$
B
)$.A.±2
B.2
C.$\pm\sqrt{2}$
D.$\sqrt{2}$
答案:
B
2. 已知一个自然数的算术平方根是a,则与该自然数相邻的较大自然数的算术平方根是(
A.$a - 1$
B.$\sqrt{a^{2}+1}$
C.$a + 1$
D.0
B
).A.$a - 1$
B.$\sqrt{a^{2}+1}$
C.$a + 1$
D.0
答案:
B
3. 一个数值转换器的原理如图所示,当输入的$x = 9$时,输出y的值是(
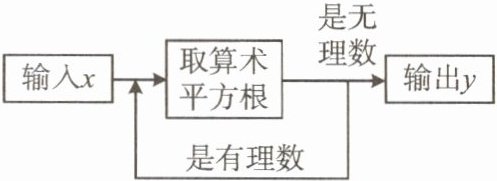
A.3
B.$\sqrt{3}$
C.$-\sqrt{3}$
D.$\pm\sqrt{3}$
B
).
A.3
B.$\sqrt{3}$
C.$-\sqrt{3}$
D.$\pm\sqrt{3}$
答案:
B
4. 已知$\sqrt{2}\approx1.414$,$\sqrt{20}\approx4.472$,则$\sqrt{2000}\approx$(
A.44.72
B.14.414
C.28.828
D.89.44
A
).A.44.72
B.14.414
C.28.828
D.89.44
答案:
A
5. 已知$\sqrt{12 - n}$是最小的正整数,则实数n的值是(
A.12
B.11
C.8
D.3
B
).A.12
B.11
C.8
D.3
答案:
B
6. $\sqrt{16}$的算术平方根是
2
.
答案:
2
7. 若x,y为实数,且$\vert x - 2\vert+(y + 1)^{2}= 0$,则$\sqrt{x + y}$的值为
1
.
答案:
1
8. 求下列数的算术平方根.
(1)225 (2)$1\frac{7}{9}$
(3)0.64 (4)3
(1)225 (2)$1\frac{7}{9}$
(3)0.64 (4)3
答案:
8.解:
(1)
∵225=15²,
∴225的算术平方根是15.
(2)
∵1 7/9=16/9=(4/3)²,
∴1 7/9的算术平方根是4/3.
(3)
∵0.64=0.8²,
∴0.64的算术平方根是0.8.
(4)3的算术平方根是√3.
(1)
∵225=15²,
∴225的算术平方根是15.
(2)
∵1 7/9=16/9=(4/3)²,
∴1 7/9的算术平方根是4/3.
(3)
∵0.64=0.8²,
∴0.64的算术平方根是0.8.
(4)3的算术平方根是√3.
9. 座钟的摆针摆动一个来回所需的时间称为一个周期,计算公式为$T = 2\pi\sqrt{\frac{h}{10}}$,其中T(s)表示周期,h(m)表示摆长.假如一台座钟的摆长为0.4m,它每摆动一个来回发出一次滴答声,那么在1min内,该座钟大约发出多少次滴答声?($\pi$取3.)
答案:
9.解:
∵T=2π√(h/10),h=0.4,
∴T=2π×√(0.4/10)≈1.2(s).
∵1 min=60 s,60÷1.2=50(次),
∴在1 min内,该座钟大约发出了50次滴答声.
∵T=2π√(h/10),h=0.4,
∴T=2π×√(0.4/10)≈1.2(s).
∵1 min=60 s,60÷1.2=50(次),
∴在1 min内,该座钟大约发出了50次滴答声.
10. 已知$\triangle ABC$的三边长a,b,c满足$\sqrt{a - 15}+(b - 8)^{2}+\vert c - 17\vert=0$,试判断$\triangle ABC$的形状,并说明理由.
答案:
10.解:△ABC是直角三角形.理由:
∵√(a-15)+(b-8)²+|c-17|=0,
∴a=15,b=8,c=17.
∵a²+b²=c²,
∴△ABC是直角三角形.
∵√(a-15)+(b-8)²+|c-17|=0,
∴a=15,b=8,c=17.
∵a²+b²=c²,
∴△ABC是直角三角形.
11. 观察下列等式:
$①\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}= 1+\frac{1}{1}-\frac{1}{2};$
$②\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}= 1+\frac{1}{2}-\frac{1}{3};$
$③\sqrt{1+\frac{1}{3^{2}}+\frac{1}{4^{2}}}= 1+\frac{1}{3}-\frac{1}{4};$
……
(1)根据以上等式提供的信息猜想:$\sqrt{1+\frac{1}{5^{2}}+\frac{1}{6^{2}}}$=
(2)猜想第n个等式为
(3)试用你所发现的规律计算$\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}+\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}+\sqrt{1+\frac{1}{3^{2}}}+\frac{1}{4^{2}}}+\cdots+\sqrt{1+\frac{1}{99^{2}}+\frac{1}{100^{2}}}$
$①\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}= 1+\frac{1}{1}-\frac{1}{2};$
$②\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}= 1+\frac{1}{2}-\frac{1}{3};$
$③\sqrt{1+\frac{1}{3^{2}}+\frac{1}{4^{2}}}= 1+\frac{1}{3}-\frac{1}{4};$
……
(1)根据以上等式提供的信息猜想:$\sqrt{1+\frac{1}{5^{2}}+\frac{1}{6^{2}}}$=
$1+\frac{1}{5}-\frac{1}{6}$
=$\frac{31}{30}$
.(2)猜想第n个等式为
$\sqrt{1+\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}}}=1+\frac{1}{n}-\frac{1}{n+1}$
.(3)试用你所发现的规律计算$\sqrt{1+\frac{1}{1^{2}}+\frac{1}{2^{2}}}+\sqrt{1+\frac{1}{2^{2}}+\frac{1}{3^{2}}}+\sqrt{1+\frac{1}{3^{2}}}+\frac{1}{4^{2}}}+\cdots+\sqrt{1+\frac{1}{99^{2}}+\frac{1}{100^{2}}}$
原式$=1+\frac{1}{1}-\frac{1}{2}+1+\frac{1}{2}-\frac{1}{3}+1+\frac{1}{3}-\frac{1}{4}+\cdots+1+\frac{1}{99}-\frac{1}{100}=100-\frac{1}{100}=99\frac{99}{100}$
答案:
11.解:
(1)1$\frac{+1}{5}$$\frac{-1}{6}$ $\frac{31}{30}$
(2)√(1+1/n²+1/(n+1)²)=1+1/n-1/(n+1)
(3)原式=1+1$\frac{-1}{2}$+1$\frac{+1}{2}$$\frac{-1}{3}$+1$\frac{+1}{3}$$\frac{-1}{4}$+…+1$\frac{+1}{99}$$\frac{-1}{100}$=100$\frac{-1}{100}$=99 $\frac{99}{100.}$
(1)1$\frac{+1}{5}$$\frac{-1}{6}$ $\frac{31}{30}$
(2)√(1+1/n²+1/(n+1)²)=1+1/n-1/(n+1)
(3)原式=1+1$\frac{-1}{2}$+1$\frac{+1}{2}$$\frac{-1}{3}$+1$\frac{+1}{3}$$\frac{-1}{4}$+…+1$\frac{+1}{99}$$\frac{-1}{100}$=100$\frac{-1}{100}$=99 $\frac{99}{100.}$
查看更多完整答案,请扫码查看


