《2025年新课堂学习与探究八年级数学上册北师大版》

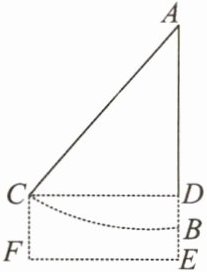
4. 勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具之一,也是数形结合的纽带之一。如图,当秋千静止时,踏板离地的竖直高度 $BE = 1.2\mathrm{m}$,将它往前推 $3\mathrm{m}$ 至 $C$ 处时(即水平距离 $CD = 3\mathrm{m}$),踏板离地的竖直高度 $CF = 2.2\mathrm{m}$,它的绳索始终拉直,则绳索 $AC$ 的长是(B)。

A.$4\mathrm{m}$
B.$5\mathrm{m}$
C.$6\mathrm{m}$
D.$8\mathrm{m}$

答案： B

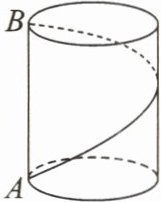
5. 如图,要从点 $A$(圆柱下底面上一点)环绕圆柱侧面建梯子到点 $A$ 正上方、圆柱上底面上的点 $B$。若圆柱底面周长为 $12\mathrm{m}$,高为 $5\mathrm{m}$,则所建梯子最短为13$\mathrm{m}$。

答案： 13

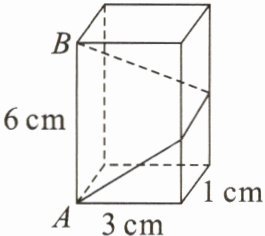
6. 如图,长方体的底面边长分别为 $1\mathrm{cm}$ 和 $3\mathrm{cm}$,高为 $6\mathrm{cm}$。如果用一根细线从点 $A$ 开始经过 $4$ 个侧面缠绕一圈到达点 $B$,那么所用细线最短需要10$\mathrm{cm}$。

答案： 10

7. 我国古代一部数学著作中有这样一道题,该题的大意是：一根竹子原来高 $1$ 丈($1$ 丈 $= 10$ 尺),一阵风将竹子折断,竹梢恰好抵地,抵地处离竹子底部 $6$ 尺远,问折断处离地面的高度是多少。设折断处离地面的高度为 $x$ 尺,则可列方程x²+6²=(10 - x)²。

答案： x²+6²=(10 - x)²

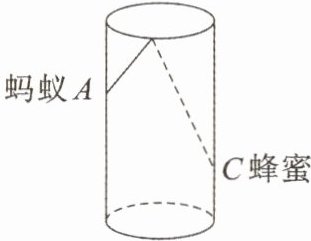
8. 如图所示圆柱形玻璃杯的高为 $12\mathrm{cm}$,底面周长为 $18\mathrm{cm}$,在杯内离杯底 $4\mathrm{cm}$ 的点 $C$ 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁距杯上沿 $4\mathrm{cm}$ 且与蜂蜜相对的点 $A$ 处。蚂蚁爬到蜂蜜处的最短距离为多少？

答案：
8. 解:如图,将杯子侧面展开,作点A 关于EQ 的对称点A',连接A'C,则A'C 即为最短距离.

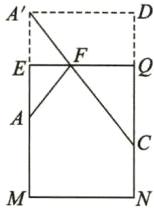
A'D=1/2×18=9(cm),CQ=12 - 4=8(cm),
CD=4 + 8=12(cm).
在Rt△A'DC 中,
由勾股定理得A'C²=A'D²+CD²=9²+12²=15²,
故A'C=15cm.
答:蚂蚁到达蜂蜜处的最短距离为15cm.