《2025年新课堂学习与探究八年级数学上册北师大版》

行程问题
(1)追击问题:同地、同向、不同时,抓路程之间的关系建立等量关系.
(2)相遇问题:同时、相向、不同地,常用的关系为两者路程和= 全程.
(3)航行问题:顺水航行的速度= 船在静水中的速度+水流速度,逆水航行的速度= 船在静水中的速度-水流速度.

答案：
(1)路程；
(2)两者路程；
(3)水流速度，水流速度

[知识点]行程问题
已知某铁路桥长 1 000 m,现有一列火车从该桥上通过,测得火车从开始上桥到完全过桥共用 1 min,整列火车完全在桥上的时间为 40 s.求火车的长度和速度.

答案： 解:设火车的长度为x m,火车的速度为y m/s,根据题意得{1000+x=60y,1000-x=40y解得{x=200,y=20.答:火车的长度为200 m,速度为20 m/s.

1. 如果一个两位数的十位数字与个位数字之和为 6,那么这样的两位数有(B).
A.3 个
B.6 个
C.5 个
D.4 个

答案： B

2. 甲、乙两地相距 360 km,一艘轮船往返于甲、乙两地之间,顺水行船用 18 h,逆水行船用 24 h.若设该船在静水中的速度为 x km/h,水流速度为 y km/h,下列方程组符合题意的是(A).
A.$\begin{cases}18(x + y)= 360,\\24(x - y)= 360\end{cases} $
B.$\begin{cases}18(x + y)= 360,\\24(x + y)= 360\end{cases} $
C.$\begin{cases}18(x - y)= 360,\\24(x - y)= 360\end{cases} $
D.$\begin{cases}18(x - y)= 360,\\24(x + y)= 360\end{cases} $

答案： A

3. 某车间有 60 名工人生产太阳镜,1 名工人每天可生产镜片 200 片或镜架 50 个.应如何分配工人生产镜片和镜架,才能使产品配套?设安排 x 人生产镜片,y 人生产镜架,则可列方程组(A).
A.$\begin{cases}x + y= 60,\\200x= 2×50y\end{cases} $
B.$\begin{cases}x + y= 60,\\200x= 50y\end{cases} $
C.$\begin{cases}x + y= 60,\\50x= 200y\end{cases} $
D.$\begin{cases}x + y= 60,\\2×200x= 50y\end{cases} $

答案： A

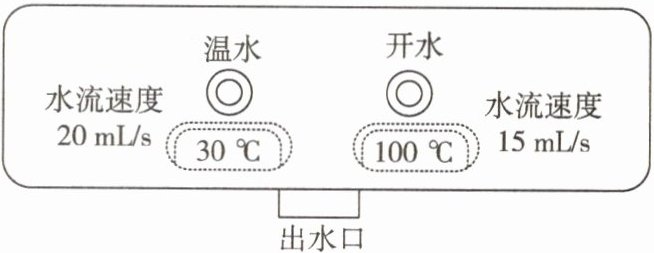
4. 某饮水机有温水、开水两个按钮,温水和开水共用一个出水口.开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量,可以得到“开水的体积×开水降低的温度= 温水的体积×温水升高的温度”.李老师拿空水杯先接了 14 s 的温水,又接了 8 s 的开水,刚好接满.小明拿空水杯先接了一会儿温水,又接了一会儿开水,得到一杯体积为 210 mL、温度为 40°C 的水(不计热损失).有下列 3 个结论:
①李老师的水杯容量为 400 mL;
②李老师接满水后,水杯中水温为 56°(不计热损失);
③小明同学的接水时间为 11 s.
其中,正确的结论是(B).

A.①②
B.①③
C.②③
D.①②③

答案： B