《2025年新课堂学习与探究八年级数学上册北师大版》

9. 为进一步落实立德树人的根本任务,培养德智体美劳全面发展的社会主义接班人,某校开展劳动教育课程,并取得了丰硕成果。如图所示是该校开垦的一块作为学生劳动实践基地的四边形荒地,$AD = 4\mathrm{m}$,$CD = 3\mathrm{m}$,$AD\perp DC$,$AB = 13\mathrm{m}$,$BC = 12\mathrm{m}$。求这块地的面积。

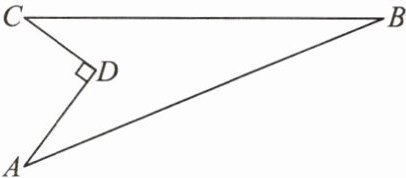
答案：
9. 解:如图,连接AC.

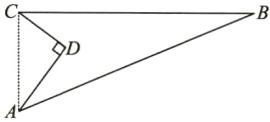
在Rt△ADC 中,根据勾股定理得AC=5m.
∵AC²+BC²=5²+12²=169,AB²=13²=169,
∴AC²+BC²=AB²,
∴△ABC 是直角三角形,
∴∠ACB=90°,
∴该田地的面积是:△ABC 的面积 - △ADC 的面积
=1/2AC·BC - 1/2AD·CD=1/2×5×12 - 1/2×4×3=24(m²).
答:该田地的面积是24m².

10. 一个长方体的透明玻璃鱼缸如图所示,长 $AD = 80\mathrm{cm}$,高 $AB = 60\mathrm{cm}$,水深 $AE = 40\mathrm{cm}$。在水面 $EF$ 上紧贴内壁 $G$ 处有一鱼饵,且 $EG = 60\mathrm{cm}$。一只小虫想从鱼缸外的点 $A$ 沿缸壁爬到鱼缸内吃鱼饵。
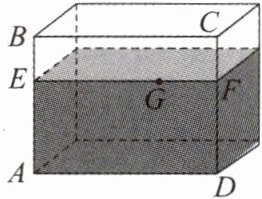
(1) 这只小虫应该怎样爬才能使路线最短？请你在图中画出它爬行的最短路线,并用箭头标注。
(2) 求这只小虫爬行的最短路线的长度。

答案：
10. 解:
(1)如图,AQ+QG 为最短路线.

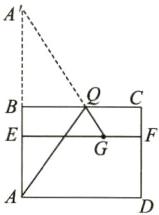
(2)在Rt△A'EG 中,
∵AE=40cm,AA'=120cm,
∴A'E=80cm.
∵EG=60cm,
∴(AQ+QG)²=(A'Q+QG)²=A'G²=A'E²+EG²=100²,
∴A'G=100cm.
故最短路线的长度为100cm.