《2025年新课堂学习与探究八年级数学上册北师大版》

14. (广安中考)在平面直角坐标系中,将函数$y = 3x + 2的图象向下平移3$个单位长度,所得图象的函数解析式是(D).
A.$y = 3x + 5$
B.$y = 3x - 5$
C.$y = 3x + 1$
D.$y = 3x - 1$

答案： D

15. (阜新中考)当我们将一条倾斜的直线上、下平移时,直线的左、右位置也发生着变化.下面是关于“一次函数图象平移的性质”的探究过程,请补充完整.
(1)如图,将一次函数$y = x + 2的图象向下平移1$个单位长度,相当于将它向右平移了1个单位长度.
(2)将一次函数$y = -2x + 4的图象向下平移1$个单位长度,相当于将它向左(填“左”或“右”)平移了$\frac{1}{2}$个单位长度.
(3)综上,对于一次函数$y = kx + b(k eq 0)$的图象而言,将它向下平移$m(m ＞ 0)$个单位长度,相当于将它向右(填“左”或“右”)$(k ＞ 0$时)或向左(填“左”或“右”)$(k ＜ 0$时)平移了$n(n ＞ 0)$个单位长度,且$m$,$n$,$k$满足等式$m=n|k|$.

答案：
(1)1
(2)左 $\frac{1}{2}$
(3)右 左 $m=n|k|$

16. (西宁中考)某校数学兴趣小组为了解新能源汽车的充电情况,对某品牌汽车进行了调查研究,绘制了如图所示的汽车电池电量$y(kW \cdot h)与充电时间x(h)$之间的函数图象,其中折线$ABC表示用快速充电器充电时y_1与x$的函数关系,线段$AD表示用普通充电器充电时y_2与x$的函数关系.
(1)用快速充电器充电时,汽车电池电量从$10 kW \cdot h充到70 kW \cdot h$需要______$h$.
(2)求$y_2关于x$的函数关系式,并直接写出自变量$x$的取值范围.
(3)该品牌汽车电池电量从$10 kW \cdot h充到100 kW \cdot h$,快速充电器比普通充电器少用______$h$.

(1)$\frac{1}{3}$
(2)$y_2=30x+10(0≤x≤3)$
(3)$\frac{7}{3}$

答案： 解:
(1)由图象可知,用快速充电器充电时,汽车电池电量从10 kW·h充到70 kW·h需要$\frac{1}{3}$h,
故答案为$\frac{1}{3}$.
(2)设$y_2$关于x的函数关系式为$y_2=kx+b(k≠0)$,
将A(0,10),E(2,70)代入上式,
得b=10,2k+b=70,k=30,
∴$y_2$关于x的函数关系式为$y_2=30x+10(0≤x≤3)$.
(3)把$y_2=100$代入$y_2=30x+10$,
得30x+10=100,解得x=3,
∴$3-\frac{2}{3}=\frac{7}{3}(h)$.
该品牌汽车电池电量从10 kW·h充到100 kW·h,快速充电器比普通充电器少用$\frac{7}{3}$h.
故答案为$\frac{7}{3}$.

17. (天津中考)在“看图说故事”活动中,某学习小组结合图象设计了如下问题情境：
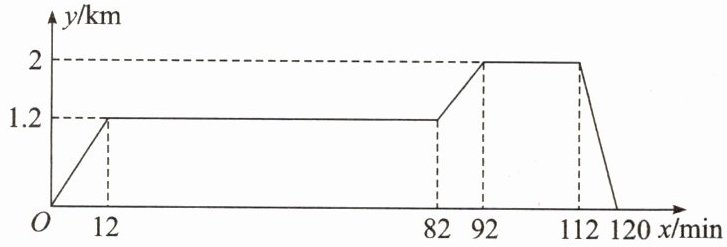
已知学生公寓、阅览室、超市依次在同一条直线上,阅览室离学生公寓$1.2 km$,超市离学生公寓$2 km$.小琪从学生公寓出发,匀速步行$12 min$到阅览室,在阅览室停留$70 min$后,匀速步行$10 min$到超市,在超市停留$20 min$后,匀速骑行$8 min$返回学生公寓.如图所示图象反映了这个过程中小琪离学生公寓的距离$y(km)与离开学生公寓的时间x(min)$之间的对应关系.
请根据相关信息解答下列问题：
(1)填表：

(2)填空：
①阅览室与超市的距离为______$km$.
②小琪从超市返回学生公寓时的速度为______$km/min$.
③当小琪离学生公寓的距离为$1 km$时,他离开学生公寓的时间为______$min$.
(3)当$0 \leq x \leq 92$时,请直接写出$y关于x$的函数表达式.

答案： 解:
(1)根据题意得:小琪从学生公寓出发,匀速步行12 min到达离学生公寓1.2 km的阅览室,
所以离开学生公寓的时间为8 min,
离学生公寓的距离是$\frac{1.2}{12}×8=0.8(km)$.
由图象可知:离开学生公寓的时间为50 min,离学生公寓的距离是1.2 km;
离开学生公寓的时间为112 min,离学生公寓的距离是2 km.
故答案为0.8,1.2,2.
(2)①阅览室与超市的距离为2-1.2=0.8(km).
故答案为0.8.
②小琪从超市返回学生公寓的速度为$\frac{2}{120-112}=0.25(km/min)$.
故答案为0.25
③当小琪从学生公寓出发,离学生公寓的距离为1 km时,他离开学生公寓的时间为$\frac{1}{1.2÷12}=10(min)$.
当小琪从超市出发,离学生公寓的距离为1 km时,他离开学生公寓的时间为$112+\frac{2-1}{2÷8}=116(min)$.
故答案为10或116.
(3)当0≤x≤12时,y=0.1x;
当12＜x≤82时,y=1.2;
当82＜x≤92时,
$y=1.2+\frac{2-1.2}{92-82}(x-82)=0.08x-5.36$.
综上,$y=\begin{cases}0.1x(0≤x≤12), \\1.2(12＜x≤82),\\0.08x-5.36(82＜x≤92).\end{cases}$